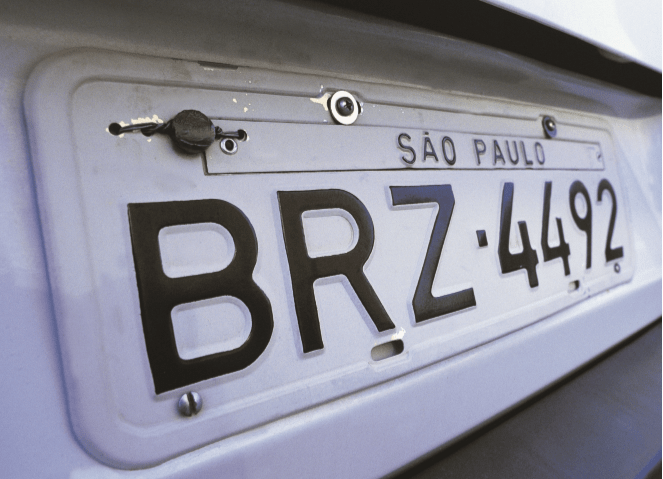Combinatória: A arte de contar e combinar

IDENTIDADE ÚNICA. Cada placa de automóvel no Brasil é criada pelo arranjo de três letras e quatro algarismos

O conjunto formado pelo arranjo de elementos de outros dois ou mais conjuntos depende do modo como esses elementos são combinados

A análise combinatória lida com o cálculo das diversas possibilidades de combinar elementos em diferentes conjuntos. Por exemplo, combinar 9 dígitos no número dos celulares, ou três letras e quatro algarismos nas placas dos automóveis. A combinatória é uma ferramenta essencial para o cálculo das probabilidades.

O número de combinações possíveis entre elementos de um ou mais conjuntos depende das condições em que essa combinação é feita. Em alguns casos, os elementos de um conjunto podem se repetir, em outros, não. Há casos, ainda, em que a ordem dos elementos do grupo é importante. Nos números de telefone, por exemplo, os algarismos
podem se repetir, e a troca de posição de um único dígito já cria um número diferente, para outro aparelho.

Árvore das possibilidades

Uma das maneiras de calcular as possibilidades para um evento é montar a árvore de possibilidades – um diagrama para calcular o número de resultados possíveis de um evento e a probabilidade de obter cada resultado.

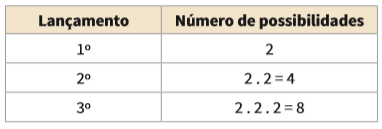
Veja a árvore de possibilidades para a sequência de três lançamentos de uma moeda. Repare que, a cada vez em que a moeda é lançada, há apenas duas possibilidades de resultado: ou dá cara, ou dá coroa. Assim, a cada novo lançamento, o número de possibilidades é multiplicado por 2.

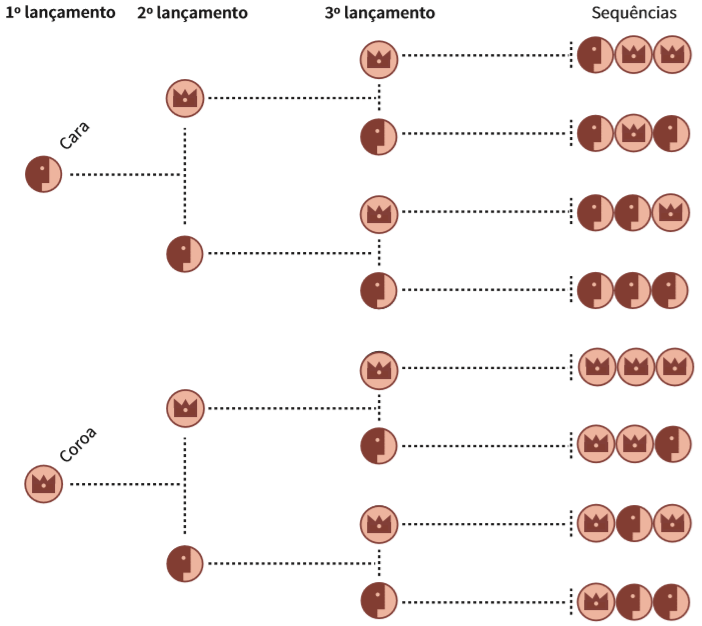
Repare que o número total de possibilidades aumenta a cada novo lançamento: às duas possibilidades para o primeiro lançamento somam- se outras duas para o segundo, e mais duas para o terceiro lançamento. Ao final dos três lançamentos, há um conjunto de oito possibilidades de resultado. Assim, o número total de possibilidades é o produto das possibilidades de cada um dos lançamentos. Este é o princípio multiplicativo. Confira abaixo:

Permutação simples

São situações em que as posições dos elementos no conjunto são importantes, ou seja, a cada troca de posição, um novo conjunto é formado. Por exemplo, a ordem de pessoas em uma fila, ou de livros em uma estante. Em todos esses casos, os elementos com que se trabalha são obrigatoriamente distintos. Em uma permutação simples de n elementos, o total de possibilidades é o fatorial de n, ou seja, n!
P(n) = n!

Em matemática,  o ponto de exclamação (!) indica fatorial –  a multiplicação de números naturais consecutivos, em ordem decrescente:

Exemplo:

O filme O jogo da imitação, de Morten Tyldum, aborda o tema combinatória. Ele conta a história do pioneiro da computação Alan Turing, que quebrou o código secreto usado pelos nazistas em suas mensagens, durante a Segunda Guerra Mundial.

ÁRVORE DAS POSSIBILIDADES

Quantos números ímpares formados por três algarismos distintos existem?

Temos dez algarismos (de 0 a 9) para distribuir por três casas: unidade, dezena e centena. Vamos casa a casa:

• – Casa das centenas: pode ser ocupada por qualquer algarismo, menos o zero (ou não teríamos um número com três algarismos). São 9 possibilidades.
• – Casa das dezenas: pode ser ocupada por qualquer algarismo, par ou ímpar, inclusive o zero. Mas esse algarismo não pode ter sido usado na casa das centenas. Ficamos então, de novo, com 9 possibilidades.
• – Casa das unidades: o enunciado diz que o número tem de ser ímpar. Portanto, essa casa só pode ser ocupada pelos algarismos 1, 3, 5, 7 ou 9. São 5 possibilidades.

O número total de número ímpares de três algarismos é a multiplicação de cada uma dessas possibilidades: 9 . 9 . 5 = 405. Existem, portanto 405 números ímpares de três algarismos distintos.

PERMUTAÇÃO SIMPLES

Quantos anagramas são possíveis da palavra  SIMULADO? 

Anagrama é a recombinação de todas as letras de uma palavra, apenas alterando sua posição. SIMULADO é formada por 8 letras distintas. Então, pela fórmula:

E quantos anagramas de SIMULADO podemos montar, mantendo as letras D e O lado a lado?
As letras D e O se comportam como uma única letra. Consideramos, então, que nossa palavra funciona como se tivesse apenas sete letras. Mas as letras D e O podem trocar de lugar entre si: DO ou OD. O total de possibilidades é:

Permutação com repetição

Ocorre quando o conjunto onde haverá permutação apresenta elementos repetidos. Nesse caso, descontamos os casos de repetição. No princípio multiplicativo, descontar significa dividir. A fórmula geral para permutação com repetição é:

• >> n é o número de elementos
• >> a, b, c… são os elementos repetidos.

Por exemplo, quantos são os anagramas possíveis da palavra COURO?
Consideramos as cinco letras, como se não houvesse repetição da letra O. Temos, então uma permutação simples:

Mas a permutação de um O com o outro não cria um novo anagrama. Então, descontando essa permutação, pela divisão: 120 : 2 = 60 anagramas.

COMBINAÇÃO SIMPLES

Em uma urna, há cinco bolas pretas e três bolas brancas. De quantas maneiras é possível, ao se sortear três bolas, que saiam duas bolas pretas e uma branca?

As bolas pretas e brancas são idênticas entre si, então a ordem em que elas são sorteadas não faz a menor diferença. Temos a combinação de dois eventos: sortear duas bolas pretas e sortear uma bola branca.

• >> Para o sorteio das pretas: 5 bolas pretas, duas a duas:
  
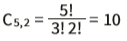
• >> Para sorteio das brancas: 3 bolas brancas, uma a uma:
  

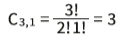
Pelo princípio multiplicativo, o número de possibilidades para o evento total é o produto dos dois eventos tomados separadamente:
10 . 3 = 30 possibilidades.

Este é o número de possibilidades de, ao sortearmos três bolas, tirarmos duas pretas e uma branca.

Arranjos

Arranjo simples é aquele que, de um grupo de n elementos distintos, queremos formar um subconjunto ordenado e único de alguns desses elementos (p):

• >> n é o total de elementos;
• >> p é o número de elementos de cada subconjunto a ser formado.

Arranjo com repetição é aquele que admite repetição. A fórmula geral para o cálculo de arranjos com repetição é:

• >> n  é o total de elementos;
• >> p é o número de elementos de cada subconjunto a ser formado.

Combinação simples

Nela, a troca de posição entre os elementos não cria um novo grupo. Ou seja, são arranjos em que não importa a ordem dos elementos. Veja o exemplo  a seguir:

De quantas formas é possível formar uma comissão de três membros, a partir de um conjunto de cinco pessoas (A, B, C, D e E)? 

Começamos tratando a situação como se fosse um caso de arranjo simples. O número de possibilidades seria 5 . 4 . 3 = 60.

Mas, nas combinações simples, a ordem não é importante (como é nos arranjos). Portanto, incluídas nas 60 possibilidades, temos seis possibilidades de permutação para cada grupo de três membros: {A, B, C}, {A, C, B}, {C, A, B}, {C, B, A}, {B, A, C} e {B, C, A}.

Para descontar essa repetição, devemos fazer a divisão do total de possibilidades pelas possibilidades repetidas – neste caso, por 6. Assim, o total de comissões possíveis de se montar nessas condições
é 60 : 6 = 10.

O número possível de combinações simples, de n elementos combinados p a p é dado por:

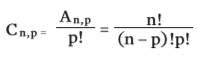
ARRANJO COM REPETIÇÃO

Quantas placas de automóvel é possível confeccionar com as regras em uso no Brasil, de três letras e quatro algarismos? (Detalhe: a legislação brasileira não permite placas com quatro zeros.) 

O alfabeto tem 26 letras e existem 10 algarismos (0 a 9). Fazendo os cálculos para cada um desses conjuntos, temos:

• >> Arranjo de 26 letras, três a três: 26 . 26 . 26 = 26³ = 17 576 possibilidades;
• >> Arranjo de 10 algarismos, quatro a quatro: 10 . 10 . 10 . 10 = 104 = 10 000 possibilidades.

Eliminando a placa 0000, ficamos com 9 999 possibilidades.

O total de possibilidades é o produto dos valores obtidos acima: 17 576 . 9 999 = 175 742 424 placas possíveis.

ARRANJO SIMPLES

A senha de um cadeado é composta de quatro algarismos distintos. Qual o número máximo de tentativas que uma pessoa que não conhece a senha deve fazer para abrir o cadeado? 

A senha faz o arranjo de 10 algarismos distintos, quatro a quatro.

Para abrir o cadeado, a não ser que o arrombador tenha sorte, ele precisará fazer 5 040 tentativas.