Relações Métricas – Geometria Básica
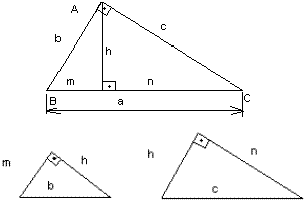
Relações Métricas no Triângulo Retângulo O triângulo ABC retângulo em A possui uma altura h que divide ABC em outros dois triângulos semelhan-tes. Usando de semelhanças entre os triângulos, demons-tram-se as seguintes relações métricas abaixo: 1ª) Cada cateto é média geométrica entre a hipotenu-sa e sua projeção. 2ª) O produto da hipotenusa pela altura […]
Relações Métricas no Triângulo Retângulo
O triângulo ABC retângulo em A possui uma altura h que divide ABC em outros dois triângulos semelhan-tes.
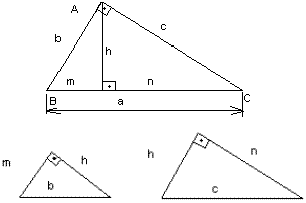
Usando de semelhanças entre os triângulos, demons-tram-se as seguintes relações métricas abaixo:
1ª) Cada cateto é média geométrica entre a hipotenu-sa e sua projeção. 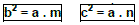
2ª) O produto da hipotenusa pela altura é igual ao produto dos catetos. 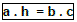
3ª) A altura é média geométrica entre as projeções dos catetos. 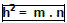
Macete! Decore e use o Quadrado Mágico.
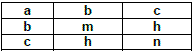
1º) Tampe uma linha e uma coluna do quadrado;
2º) Faça o produto cruzado entre as proporções restantes e aí aparecerão as relações métricas acima.
Teorema de Pitágoras O quadrado da hipotenusa é igual a soma dos quadrados dos catetos.
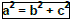
Dica! Esse teorema e suas conseqüências são muito cobradas nos vestibulares; é interessante saber as duas relações seguintes:
Altura do Triângulo Equilátero: 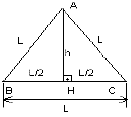
Aplicando Pitágoras no triângulo ACH, temos:
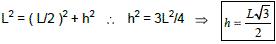
Diagonal do Quadrado:
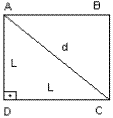
Aplicando Pitágoras no triângulo ACD, temos:
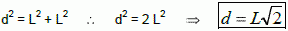
(FUVEST) Na figura a seguir, os quadrados ABCD e EFGH têm, ambos, lado a e centro O.
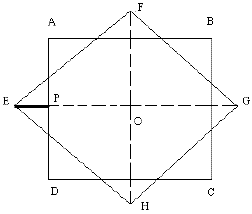
Se EP = 1, então a é :
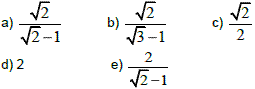

Relações Métricas no Círculo
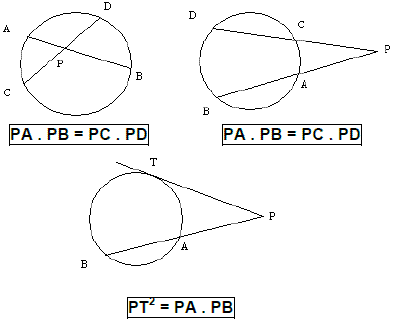
(UFMG) Observe esta figura:
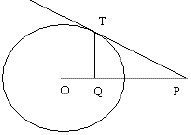
Nessa figura, o círculo tem centro O e raio 6 e OP = 16. A reta PT é tangente ao círculo em T e o segmento TQ é perpendicular à reta OP.
Assim sendo, o comprimento do segmento QP é:
a) 13,75
b) 13,85
c) 14,25
d) 14,5



 5 dicas preciosas para aprender melhor, segundo uma cientista
5 dicas preciosas para aprender melhor, segundo uma cientista O problema simples da matemática que pode não ter solução
O problema simples da matemática que pode não ter solução Uma lista com as 6 melhores cadeiras para estudar
Uma lista com as 6 melhores cadeiras para estudar “Místico” ou “mítico”: qual é o certo?
“Místico” ou “mítico”: qual é o certo? Confira redações nota mil do Enem 2023
Confira redações nota mil do Enem 2023