Probabilidade: Questão de sorte (ou azar)

FEZINHA DIFÍCIL. São mínimas as probabilidades de ganhar num jogo como a Mega-Sena, que permite milhões de combinações.

Ganhar na loteria ou ter um filho homem são eventos que dependem do acaso. Mas sempre podemos estimar as probabilidades

As possibilidades, já vimos, são todos os possíveis resultados de um evento. Probabilidade é outra coisa: a chance de que determinado resultado ocorra. Toda probabilidade é uma proporção, apresentada como porcentagem, ou como uma chance a cada x vezes. Ou seja, a probabilidade de ocorrer um evento é uma fração de todos os possíveis resultados.

Conceitos

As probabilidades são calculadas para experimentos aleatórios – aqueles que, se repetidos, têm resultados incertos, mas com a mesma chance de ocorrer. Por exemplo, não importa quantas vezes um dado é lançado, só existem seis possibilidades de resultado: 1, 2, 3, 4, 5 ou 6. E que resultado dará é um evento impossível de prever com certeza.

Todo cálculo de probabilidade envolve dois tipos de conjuntos. O espaço amostral (S) é o conjunto de possibilidades, possíveis resultados. O evento (E) é o conjunto dos resultados desejados. Quando temos um experimento aleatório, a probabilidade de E ocorrer é dada pela fração:

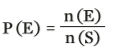
em que n é o número de eventos.

• >> Se n(E) = n(S), o evento tem probabilidade 1 = 100%. Este é chamado um evento certo;
• >> S e n(E) = 0, então P(E) = 0 = 0 %; este é um evento impossível.

Tipos de eventos

Eventos independentes – são aqueles em que a ocorrência de um não interfere na possibilidade de ocorrer o outro. Pelo princípio multiplicativo, o número de possibilidades de um evento A ocorrer e de outro evento B também ocorrer é igual ao produto das possibilidades de cada um deles ocorrer separadamente:

Dois eventos A e B são complementares se a intersecção dos conjuntos de possibilidades for vazio e se a união dos dois for igual ao espaço amostral S. Veja:

Em eventos complementares, a soma das probabilidades dos dois eventos  (A e B) é sempre igual a 100%:

Eventos mutuamente exclusivos são aqueles nos quais a ocorrência de um elimina qualquer probabilidade de ocorrer o outro. Por exemplo: qual a probabilidade de você sortear um número que seja par, primo e maior que 5? Nenhuma, porque o único número primo par é 2, que é menor que 5. Acima de 2, todos os primos são ímpares.

União de dois eventos

Possibilidades e probabilidades envolvem conjuntos. E a teoria dos conjuntos ajuda, muitas vezes, a resolver problemas nessa área. A união de dois eventos A e B é dada pela expressão:

UNIÃO DE EVENTOS

Em uma reunião de 50 homens, 20 estão de gravata, 25 estão de colete e 15 usam gravata e colete. Ao sortear ao acaso um desses homens, qual é a probabilidade de ele vestir colete ou gravata? Vamos representar os conjuntos por um diagrama de Venn.

• >> O espaço amostral (ou universo) é S = 50;
• >> Desse total, 20 estão de gravata (vamos chamar de conjunto A) e 25, de colete (conjunto B);
• >> Entre esses dois conjuntos, está A ∩ B, de homens que estão de gravata e, também, de colete (15);
• >> E outros 20 não estão nem de gravata, nem de colete.

Para encontrar o número de homens com gravata ou colete (união de A e B), soma- mos os elementos de A e B: 20 + 25 = 45. Mas temos de eliminar aqueles que estão, ao mesmo tempo de gravata e de colete  (o conjunto A ∩ B).
Então 45 – 15 = 30.
A probabilidade de sortear um desses 30 homens é dada pela fração:

Veja o diagrama de Venn com os valores:

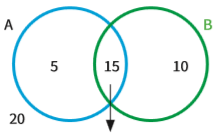
Repare que fora dos conjuntos A e B estão 20 homens que não usam nem gravata, nem colete. O espaço amostral é a soma de todos os valores: 20 + 5 + 15 + 10 = 50.

MÉDIAS, MEDIANA E MODA

A combinatória e a probabilidade estão na base das estatísticas – a coleta e organização de dados que fazem um retrato de determinada situação. A estatística estuda uma amostra, que é parte de um universo de elementos. Por exemplo, para estudar o desempenho de todos os 240 alunos de dez classes do Ensino Médio, os diretores de uma escola podem selecionar oito alunos de cada sala. O universo é o total de alunos da escola: 240. E a amostra é a soma dos alunos selecionados: 80. Numa amostra significativa, que represente o universo, é possível estabelecer relações que podem ser extrapoladas para o universo. Conheça  alguns conceitos básicos usados na estatística:

• >> Médias: Existem dois tipos de médias. A média aritmética é a soma de todos os valores dos elementos de um conjunto dividida pelo número total de elementos de um conjunto. Na média ponderada, levamos em consideração o peso de cada elemento (por exemplo, provas com peso 2
  ou 1). Neste caso, o cálculo é multiplicar cada elemento por seu peso, somar todos eles e dividir o resultado pela soma de todos os pesos.

• >> Mediana: é a medida central de uma lista de medidas colocadas em ordem crescente, ou decrescente. Quando temos um número ímpar de valores, a mediana é exatamente o valor central. Quando o número de valores é par, a mediana é a média aritmética dos dois valores centrais.

•  >> Moda: é o valor que mais aparece em uma série de dados.

MÉDIA, MEDIANA E MODA

As notas dos alunos de uma classe são 4, 2, 9, 5, 6, 2, 7, 2, 6 .

• A média aritmética das notas é a soma das notas dividida pelo total de notas: 4 + 2 + 9 + 5 + 6 + 2 + 7 + 2 + 6 / 9 = 43/9 = 4,7
• Para encontrar a mediana, devemos colocar as notas em ordem crescente: 2, 2, 2, 4, 5, 6, 6, 7, 9
  A mediana é a nota no centro da lista: Med = 5
• A moda é mais fácil ainda de ser definida: é a nota que aparece mais vezes na lista: 2

PRATICAMENTE IMPOSSÍVEL

Jogos de loteria são eventos aleatórios que podem ser considerados jogos de azar porque as chances de ser contemplado são muito pequenas. A Mega-Sena, por exemplo: para vencer, o apostador tem de acertar a combi- nação de seis números num espaço amostral de 60 números.

A probabilidade de acertar com uma aposta simples, de 6 números, é calculada assim:

Qual a chance de fazer a Mega-Sena apostando em apenas seis números?
O primeiro passo é verificar qual o número total de possibilidades de aposta, ou seja, quantas combinações de seis números o apostador pode fazer, entre 1 e 60.  Lembre que:

•  n = 60  (total de elementos do conjunto)

• = 6 (número de elementos que devem ser combinados a cada vez)
• 
  O fatorial de 60 indica a multiplicação de todos os números naturais, em ordem decrescente, do 60 até 1. Então:
• 60! = 60 . 59 . 58 . 57 . 56 . 55 .(…) . 3 . 2 . 1

Uma vez que podemos indicar o fatorial em qualquer ponto da operação, simplificamos a divisão:

60! = 60 . 59 . 58 . 57 . 56 . 55 . 54!


Fazendo as simplificações:


Portanto, na Mega-Sena é possível obter  50 063 860 combinações de seis números escolhidos entre 1 e 60.
Essas são todas as possibilidades. Calculemos, agora, a probabilidade de serem sorteados exatamente os seis números em que se apostou.

Ou seja, do total de 50 063 860 possibilidades, só um resultado é válido. Então, a probabilidade de acertar a sena é de 1 em 50 063 860:

A chance de acertar a sena é, aproximadamente, de 1 em 50 milhões de apostas.

Qual a chance de fazer a quina (acertar cinco números) apostando apenas em seis números?
Calculamos, primeiro, as possíveis combinações dos seis números sorteados, cinco a cinco:

Existem seis possíveis combinações dos seis números sorteados, cinco a cinco. Só que cada uma dessas seis possíveis combinações deve “casar” com um sexto número que não será sorteado.

Se a cada concurso são sorteados seis números dentre 60, o total de números não sorteados é 54. Existem, então, 54 possibilidades de apostar num número não sorteado. Em linguagem matemática:

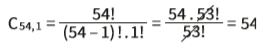
Finalmente, calculemos o total de possíveis combinações de cinco números que devem ser sorteados e um que não deve ser sorteado:

Isso significa que, em cada concurso da Mega-Sena, o apostador tem 324 possíveis combinações de cinco números entre os seis sorteados e um que não será sorteado.

Agora, vamos calcular a probabilidade de acertar cinco números. Para fazer a quina, é preciso que os seis números sorteados coincidam exatamente com uma dessas 324 possibilidades. Ou seja, é preciso que uma – e apenas uma – dessas 324 possibilidades seja sorteada, do total de 50 063 860 possíveis resultados do sorteio:

Então, a chance de alguém acertar a quina é de aproximadamente 1 a cada 150 000 apostas – ou seja, de 0,00065%.

Por fim, qual a chance de alguém fazer a quadra (acertar quatro números) apostando em seis números?

Seguindo o mesmo raciocínio desenvolvido para a quina, a aposta deve ter exatamente 4 dos 6 números sorteados (C₆,₄) e 2 entre os 54 não sorteados (C_54,2).

Assim, o número de combinações possíveis para uma quadra é dado pela expressão:

Fazendo as simplificações:

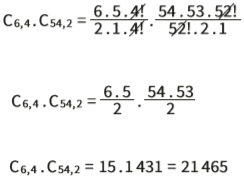
Portanto, o apostador tem 21 465 combinações possíveis para fazer a quadra. A aposta só será vencedora se for sorteada exatamente uma dessas 21 465 combinações, entre todas as 50 063 860 possibilidades do sorteio:

Então, a chance de um apostador fazer a quadra num concurso da Mega-Sena é de 1 em 2 332 vezes, ou seja, cerca de 0,043%.