Conjuntos numéricos: Conceitos fundamentais
Conheça as ferramentas básicas usadas em todas as operações, da simples contagem aos cálculos mais complexos
VIAGEM NO TEMPO Milênios se passaram desde a criação dos algarismos indo arábicos, na índia. Mas até hoje, por mais avançada que seja a tecnologia, são estes os algarismos que usamos no dia a dia
Assim como qualquer campo do conhecimento – física, química, história ou geografia –, a matemática tem também sua própria linguagem, composta de símbolos e conceitos. O primeiro e mais importante deles são os números. Sem eles, não seria possível contar, medir, ordenar e classificar.
Não se sabe ao certo que povo desenvolveu a ideia abstrata de número. Mas os historiadores têm como certo que o conceito surgiu da necessidade de contar objetos e seguir um calendário. O sistema de contagem deve ter se iniciado com o uso dos dedos, há milhares de anos, e de pedras, uma para cada unidade. Depois vieram pequenas placas de argila –, cada uma delas também representando uma unidade. Os incas criaram os quipus, um sistema de cordas e barbantes com nós.
Os numerais, ou algarismos – os símbolos gráficos que representam os números –, teriam aparecido bem mais tarde, com a escrita. E a uma certa altura da história, o comércio criou a necessidade de se registrar e comunicar a contagem de mercadorias e seus valores. Antropólogos têm registro de ossos, pedras e pedaços de madeira de pelo menos 5 mil anos com marcas escavadas com o que eles supõem tenham sido os primeiros numerais.
Atribui-se aos egípcios a invenção dos primeiros símbolos numéricos mais formais, na forma de hieróglifos. Os romanos criaram os algarismos romanos: I, V, X, L, C, D e M. Hoje a matemática faz uso, no mundo todo, dos algarismos indo arábicos: 1, 2, 3… 10, 11, 12… Acredita-se que esses algarismos tenham sido criados na Índia, também há milhares de anos.
Os números utilizados em contagens são chamados números concretos – cada número representa certa quantidade de “coisas” reais. O zero, que representa a ausência, o nada ou o vazio, não é um número concreto, mas um numeral de posição. Dependendo do local em que o zero é colocado, os numerais anteriores ou posteriores assumem diferentes valores. Por exemplo, no sistema decimal, que tem como base o 10, o numeral 1 representa uma unidade. Mas, seguido de um zero (10), são dez unidades; e 0,1 representa um décimo de uma unidade.

ALGARISMOS ROMANOS
O sistema de notação por algarismos romanos – que empregamos hoje apenas para classificar e ordenar elementos, como nos capítulos de um livro – dispensa o número zero. Nele, as letras I, V, X, L, C, D e M simbolizam quantidades básicas: 1, 5, 10, 50, 100, 500 e 1000, respectivamente. A posição e o número de vezes em que cada um desses símbolos é repetido definem dezenas, centenas e milhares.
Conjuntos
A teoria dos conjuntos é uma área da matemática que você não precisa conhecer com profundidade para o Enem. Mas seus conceitos são fundamentais para compreender enunciados e, assim, chegar à resposta correta das questões. Conjunto, você sabe: é um grupo de elementos:
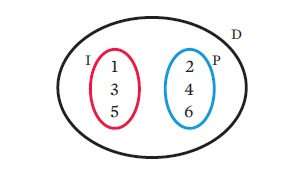
– o conjunto formado pelos números nas faces de um dado é D = {1, 2, 3, 4, 5, 6};
– já o conjunto dos números pares de um dado é P = {2, 4, 6};
– e o conjunto dos ímpares é I = {1, 3, 5}.
Os conjuntos também podem ser representados pelo diagrama de Venn. Os diagramas para os conjuntos D, P e I, acima, são:
Observe o diagrama e repare:
– O número 6 pertence (∈) aos conjuntos D e P. Então, 6 ∈ D e 6 ∈ P;
– Mas o número 3 não pertence (∉) a P. Então, 3 ∉ P;
– Todos os elementos de P e de I estão contidos (⊂) em D. Então, P ⊂ D e I ⊂ D.
– No sentido inverso, D contém (⊃) P e I. Então, D ⊃ P e D ⊃ I. Podemos fazer diversas operações entre conjuntos:
– A união (∪) é a combinação dos elementos dos conjuntos. No nosso exemplo, I ∪ P = {1, 2, 3, 4, 5, 6} = D.
– A intersecção (∩) é o conjunto formado por elementos comuns aos conjuntos. No caso do exemplo dos números pares e ímpares de um dado, o conjunto da intersecção entre I e P é um conjunto vazio (nenhum número é ímpar e par ao mesmo tempo): I ∩ P = Ø

O conjunto C resultante da união de A e B contem os elementos que se encontram em A ou em B. Já o conjunto D resultante da intersecção de A e B contem os elementos que se encontram ao mesmo tempo em A e em B.
Conjuntos numéricos
Os números também podem ser agrupados em conjuntos:
– O conjunto dos números naturais (N) é N = {0, 1, 2, 3…}. Repare que este conjunto é infinito.
– O conjunto dos números inteiros (Z) reúne os números naturais e seus opostos: Z = {…, -3, -2, -1, 0, 1, 2, 3, …}. Este também é um conjunto infinito.
– O conjunto dos números racionais (Q) é a união dos números inteiros e as frações resultantes da divisão entre quaisquer deles: Q = { | a ∈ Z e b ∈ Z*}. Traduzindo: o conjunto Q é formado pelos números obtidos pela divisão de a por b, tal que (|) a pertence ao conjunto dos números inteiros e b pertence ao conjunto dos inteiros com exceção do zero (Z*). O número b não pode assumir o valor zero porque a divisão por zero não é definida.
– O conjunto dos números irracionais (I) é o dos números que não podem ser obtidos da razão entre dois números inteiros. O π é um número irracional. A raiz de alguns números também é um número irracional – por exemplo, √2 e √3.
A união entre todos os conjuntos de números acima forma o conjunto dos números reais (R). No diagrama de Venn, essa união é representada assim: 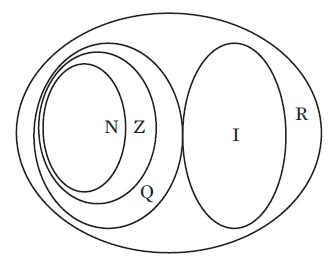 A teoria dos conjuntos é frequentemente utilizada em álgebra, principalmente em inequações, e em probabilidade.
A teoria dos conjuntos é frequentemente utilizada em álgebra, principalmente em inequações, e em probabilidade.