Eletricidade: Leis de Ohm e potência

Rastro luminoso. A intensidade da luz produzida pelos faróis de um automóvel depende da potência deles.
A dificuldade criada pelo resistor
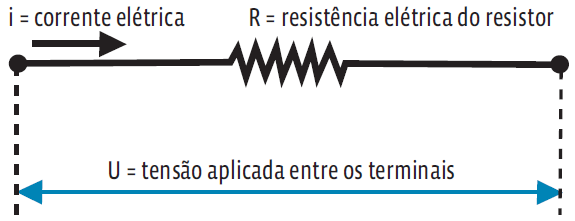
Em meados do século XIX, George Ohm fez uma série de experimentos e percebeu que, num grande número de resistores (principalmente nos resistores metálicos), a corrente elétrica é diretamente proporcional à tensão aplicada. Quanto maior a tensão, maior a corrente elétrica. Ele notou também que a constante que define a proporção entre tensão e corrente é a medida de resistência elétrica do resistor. Essa é a primeira lei de Ohm, que rege os chamados resistores ôhmicos. A expressão matemática dessa lei é:
![]() , em que:
, em que:
- U é a tensão aplicada entre os terminais do resistor, medida em volts (V);
- R é a resistência do resistor, em ohms (Ω);
- i é a corrente elétrica que atravessa o resistor, medida em ampères (A).
George Ohm (1789-1854): Físico e matemático alemão, estabeleceu as relações matemáticas entre tensão, resistência e corrente elétrica. Suas descobertas estão na base da construção dos circuitos, componentes essenciais dos equipamentos elétricos e eletrônicos dos séculos XX e XXI.
Com a primeira lei de Ohm, definimos a tensão aplicada num resistor qualquer, calculando o produto de sua resistência pela intensidade da corrente que o atravessa.
Em outras palavras, a primeira lei de Ohm estabelece que em todo resistor ôhmico a resistência elétrica permanece constante, independentemente da tensão aplicada sobre ele. O gráfico da tensão pela corrente em um resistor ôhmico é uma reta que passa pela origem dos eixos. E a resistência é o coeficiente angular da reta. Veja:

Segunda lei de Ohm
Os fios metálicos de circuitos elétricos não são ideais – são condutores, mas oferecem certa dificuldade ao movimento dos elétrons. A segunda lei de Ohm afirma que a resistência elétrica oferecida por um fio metálico é proporcional a seu comprimento ( l =, na figura abaixo) e inversamente proporcional à área de sua seção transversal (A). Depende, também, do material de que é feito o condutor.

Um cientista anota os valores da corrente elétrica que atravessa um resistor, em função da tensão aplicada sobre ele. Com esses valores, ele constrói o gráfico abaixo. Vamos verificar se o dispositivo estudado pelo cientista é um resistor ôhmico.

O gráfico é uma reta. Então, a resistência do dispositivo se mantém constante, independentemente da tensão aplicada. Portanto, o resistor é ôhmico, sim.
Para um resistor ôhmico, calculamos a resistência aplicando a equação da primeira lei de Ohm a qualquer ponto da reta.
Para o ponto de coordenadas (20, 0,4), temos:
![]()
Então:
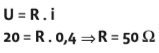
Este é o valor da resistência do resistor em questão: 50 Ω
Coeficiente angular de uma reta
Toda reta é definida por uma função de 1º grau, que tem como forma geral y = ax + b. O coeficiente angular da reta – ou seja, o valor que define o ângulo da reta com o eixo x – é a (coeficiente de x). No gráfico, o valor de a é dado por:

A expressão matemática da segunda lei de Ohm é:
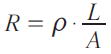 , em que:
, em que:
- l é o comprimento do condutor, medido em metro (m);
- A é a área de seção transversal do condutor cilíndrico, em metro quadrado (m2);
- t é a resistividade do material de que é feito o condutor, medida em ohms por metro (Ω . m), no S.I.
Repare que, quanto maior for o comprimento do condutor, maior será a resistência elétrica oferecida. Isso é natural, pois, quanto mais comprido for o “caminho”, maior será a barreira enfrentada pelos elétrons em seu deslocamento. Por outro lado, quanto maior for a área de seção transversal, mais elétrons passarão por ela – ou seja, menor será a resistência imposta pelo condutor.
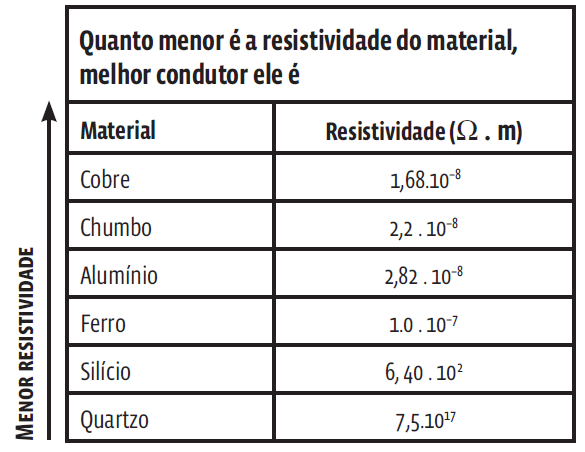
Reforçando: a resistência elétrica depende, além das características espaciais do condutor, também da resistividade do material de que o condutor é construído. Ou seja, resistividade é uma característica própria de cada material. Um fio de cobre de 1 metro de comprimento tem resistência elétrica diferente da de um fio de cobre de 2 metros de comprimento. Mas a resistividade dos dois fios é a mesma – a do cobre. Veja abaixo uma tabela com a resistividade de alguns materiais:
Associação de resistores
Geralmente, um circuito elétrico é composto de dois ou mais resistores, que podem estar associados de várias maneiras. Para simplificar o estudo de um circuito, seja qual for o número de resistores que ele contenha, podemos reduzir a associação de resistores a um único resistor – o chamado resistor equivalente – sem modificar as características gerais do circuito.
Associação em série
Resistores estão associados em série quando são conectados em sequência, de modo que todos sejam percorridos por uma mesma corrente elétrica. Veja:
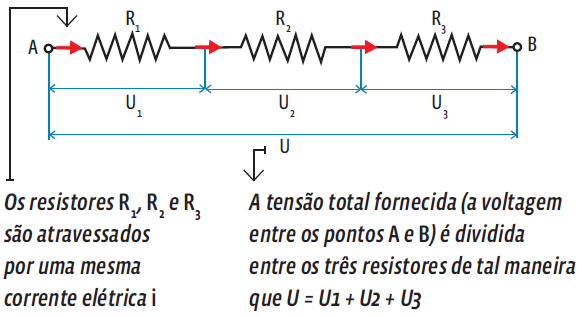
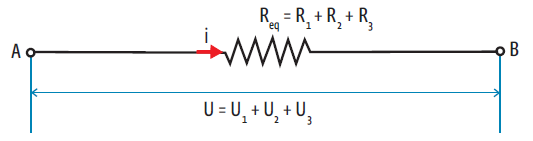
Essa associação de resistores em série pode ser substituída por um resistor equivalente. Em qualquer associação em série, o resistor equivalente tem resistência igual à soma algébrica de todas as resistências existentes no circuito.
De forma geral, num circuito com n resistores, o resistor equivalente imporá uma resistência de
![]()
O resistor equivalente dos três resistores associados em série do circuito com que trabalhamos acima seria, então:
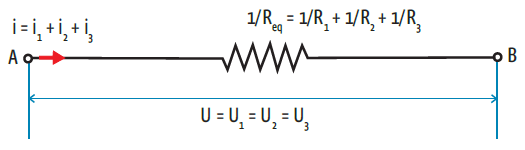
Associação em paralelo
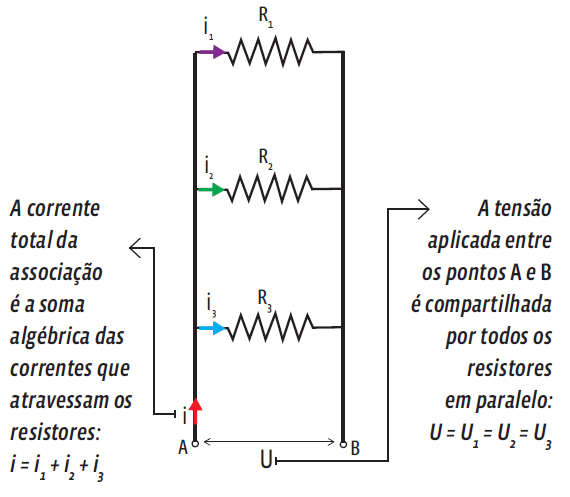
É a associação em que os resistores têm as extremidades conectadas aos mesmos pontos. Veja:
Retomando a primeira lei de Ohm, verificamos que, quanto menor a resistência, maior a corrente:
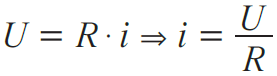
Como na associação em paralelo a tensão U é constante, concluímos que os ramos da ligação em paralelo que apresentam menor resistência elétrica serão percorridos por maior corrente.
Em circuitos com resistores também em paralelo, podemos substituir a associação de resistores por um resistor equivalente. A resistência do resistor equivalente de uma associação em paralelo é a soma algébrica do inverso das resistências elétricas do circuito inteiro.
Genericamente, num circuito com n resistores associados em paralelo, o resistor equivalente imporá uma resistência de:

Potência elétrica
Aparelhos elétricos sempre convertem energia elétrica em alguma outra forma de energia – em energia mecânica numa batedeira e num liquidificador, em energia térmica num chuveiro. A quantidade de energia elétrica que um
aparelho consegue converter por unidade de tempo é chamada potência elétrica. Matematicamente:
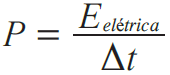 , em que:
, em que:
- P é a potência elétrica do aparelho, medida em watt (W);
- E elétrica é a energia elétrica consumida pelo aparelho, em joules (J);
- Dt é o tempo que o aparelho permanece ligado, em segundos (s).
Também podemos calcular a potência elétrica de um aparelho em função da corrente elétrica, da resistência e da tensão desse aparelho, com uma das equações abaixo:
![]()
A unidade utilizada para medir a energia elétrica consumida mensalmente numa residência é o quilowatt-hora (kW.h). E a quantidade de energia elétrica consumida em cada mês sai da equação de potência:

Então, 1 kW.h é a energia elétrica consumida por um aparelho de 1 kW (1 000 W) de potência quando permanece uma hora ligado.
A relação de conversão entre kW.h e joule é 1 kW.h = 3,6 . 106 J.
Com a equação de potência, pode-se calcular, também, o consumo mensal de qualquer eletrodoméstico. Basta verificar a potência do equipamento, em kW.h, e multiplicar esse valor pelo número de horas que o aparelho permanece ligado num mês.
AMPERÍMETRO

É o equipamento que mede a intensidade da corrente elétrica num circuito. Para isso, o amperímetro dever ser ligado ao circuito sempre em série (lembre-se de que, em ligações em série, a corrente i é constante). Ou seja, seus fos devem integrar o circuito como mais um dispositivo na sequência dos resistores já existentes no circuito. E, para ser um amperímetro ideal, ele deve oferecer resistência nula à passagem da corrente.

VOLTÍMETRO

Mede a tensão, ou a diferença de potencial, entre dois pontos de um circuito elétrico. O voltímetro deve ser sempre conectado em paralelo ao componente elétrico em questão (lembre-se: em ligações em paralelo, a tensão U se mantém constante). O voltímetro ideal é aquele que não interfere na medição da tensão do circuito porque tem uma resistência infinita. Assim, não passa praticamente nenhuma corrente pelo voltímetro, e ele mede a diferença de potencial antes e depois de um resistor.











