Função e equação de 1º grau

CADA VEZ MAIS VELHA Os gráficos que mostram a proporção de jovens e idosos na população brasileira são a representação de funções do 1º grau
A construção de uma reta
Em um gráfico, cada ponto de uma reta é dado por um par ordenado, definido por uma função de 1º grau
Todo gráfico de linha é composto de segmentos de retas desenhados no plano cartesiano, em que cada ponto é definido por um par ordenado (x , y) – ou seja, a cada valor de x, no eixo horizontal (das abscissas) existe um único valor y, no eixo vertical (das ordenadas). Em linguagem matemática, dizemos então que y é uma função de x. Acompanhe no gráfico mais abaixo, que mostra a razão de dependência no Brasil.
→ Repare que entre 1970 e 2020, a reta é decrescente. Mas, a partir de então, a reta sobe. Isso ocorre porque, até 2020, os valores de y caíram e, desse ano em diante, esses valores sobem.
→ As retas pontilhadas em vermelho são construídas unindo apenas os pontos extremos de cada um desses dois períodos: 1970 a 2020, e 2020 a 2050.
→ Repare que as retas pontilhadas não passam exatamente sobre todos pontos originais do gráfico. Então, seus valores, para cada década, não estão marcados de maneira precisa. Mas essa reta tracejada mostra a variação da dependência, entre os anos extremos – de 1970 a 2020 e, depois, de 2020 a 2050. Calculando a taxa de variação:
-
- → A razão de dependência é y, a variável;
- → y varia em função do tempo (década a década). Chamamos o tempo de x. Para cada valor de x temos um único valor de y;
- → Escolhemos pontos em que a reta coincide com os pontos originais da reta: 1970, 2020 e 2050. E, com isso, montamos a tabela com os valores correspondentes: sta é a queda da razão de dependência entre 1970 e 2020.
Fazendo o mesmo raciocínio para o período seguinte, entre 2020 e 2050, temos:
- ∆x = 3 décadas.
- ∆y = 75,1 – 50,9 = 24,2
- Taxa de variação da dependência no período:
![]()
Interpretando os valores:
- → Entre 2020 e 2050, a razão de dependência deverá aumentar num ritmo ligeiramente maior que a queda registrada entre 1970 e 2020: crescimento de 8% e queda de 7%.
- → Ao fazer o cálculo para as taxas de variação, descobrimos a função geral que define a relação entre y e x para cada período:
∆y (1970-2020) = -7 . x
∆y (1970-2020) = 8 . x
As expressões de ∆y que acabamos de encontrar são funções do 1° grau. Esse tipo de função tem sempre a forma f(x) = a . x + b
Repare que f(x) é outra maneira de representar a variável y.
O nome “função de 1° grau” vem do fato de que x é elevado à primeira potência (elevado a 1). O valor de b é o chamado coeficiente linear da reta.
Gráfico da função de 1° grau
Toda função de 1° grau tem como gráfico uma reta. Mas cada função define uma reta específica, com características próprias. Essas características dependem da relação estabelecida entre x e y, que, por sua vez, têm relação com o coeficiente angular e o coeficiente linear. Acompanhe no exemplo a seguir:
Considere a função f(x) = 2 . x – 1.
Para construir o gráfico dessa função, começamos montando uma tabela que atribui valores aleatórios a x e o valor correspondente de y.
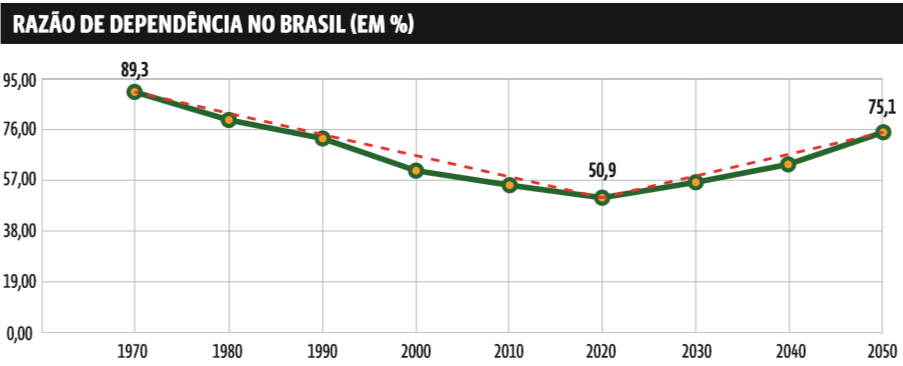
CADA VEZ MAIS DEPENDENTES A linha em verde mostra a razão de dependência – a proporção entre idosos e crianças (dependentes) e as pessoas em idade de trabalhar (que sustentam os dependentes), entre 1970 e 2050. Veja que a razão cai entre 1970 e 2020, para então começar a subir. Cada um dos pontos das linhas verdes representa um valor exato da razão na década correspondente. Já as retas pontilhadas não fornecem os valores exatos da razão em cada década, mas dão uma boa ideia da taxa de variação dessa razão nos dois períodos.
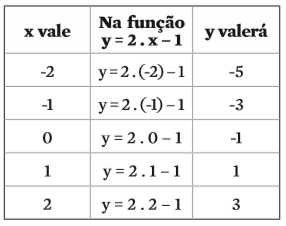
Definimos, assim, os pares ordenados desses cinco pontos:

Abaixo você vê como esses pares ordenados se organizam no gráfico.
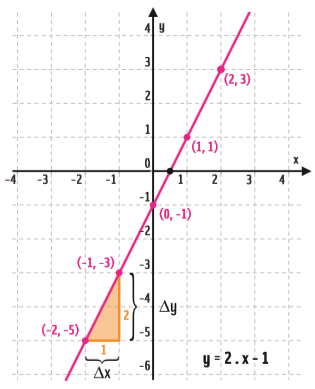
Veja que os cinco pontos interligados formam a reta da função y = 2 . x – 1.
Observe que:
- → Todos os pontos estão alinhados, formando uma reta. Na verdade, para definir qualquer reta, precisamos de apenas dois pontos. Então poderíamos ter calculado apenas os valores de y para dois valores diferentes de x;
- → Quando passamos de um ponto a outro, deslocamos uma unidade na horizontal e duas unidades na vertical. Ou seja: para ∆x = 1, ∆y = 2. Essa relação é válida para quaisquer pontos da reta;
- → No ponto em que a reta cruza o eixo y, a coordenada x vale 0 e a coordenada y vale -1.

GRÁFICO DA FUNÇÃO DE 1° GRAU
Considere outra função: f(x) = – 3 . x + 4.
A tabela para a construção do gráfico no plano cartesiano é:
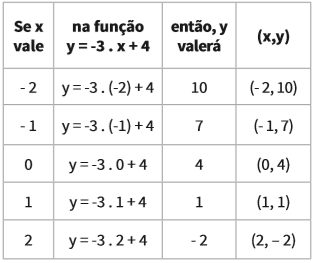
Observe que:
- → Desta vez, ao passarmos de um ponto a outro da tabela – por exemplo, de (– 2, 10) a (– 1, 7) –, andamos uma unidade para a direita no sentido horizontal (do eixo x) e 3 unidades para baixo no sentido vertical (do eixo y). Ou seja, para ∆x = 1, ∆y = – 3. Essa relação é válida para quaisquer pontos da reta;
- → No ponto em que a reta cruza o eixo y, a coordenada x tem valor 0 e a y, 4.
Novamente, com cada uma dessas coordenadas cartesianas (x, y), localizamos os pontos e traçamos a reta:
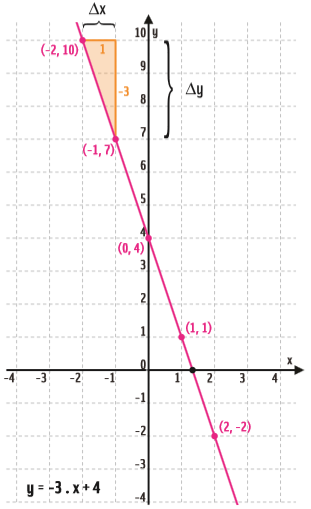
Coeficiente linear
Na função y = a . x + b, a letra b é o coeficiente linear da reta. Este é o valor de y quando x = 0. Ou seja, é o valor de y no ponto em que a reta cruza o eixo y.
- → Na função com que trabalhamos, y = 2 . x – 1, b vale -1 E no gráfico você confirma: a reta cruza o eixo x em y = -1;
- → No quadro Na prática, ao lado, no gráfico da função y = -3 . x + 4, b = 4. Confirme: a reta cruza o eixo y em y = 4.
Coeficiente angular
Nas funções dos dois exemplos citados acima, o coeficiente a é a razão da variação de y e x – ou seja, quanto y varia a cada variação de x.
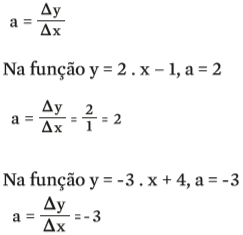
O coeficiente a é o coeficiente angular da reta. Ele define a inclinação ou declividade da reta. Para encontrar o coeficiente angular de uma reta, precisamos apenas das coordenadas de dois pontos (xA, yA) e (xB, yB) e estabelecer a razão entre suas diferenças: 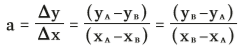
As funções do 1° grau com coeficiente angular a > 0 são crescentes e suas retas formam ângulo entre 0° e 90° com o lado positivo do eixo x.
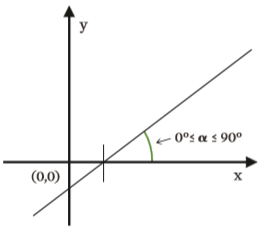
Já as funções de 1° grau com coeficiente angular a < 0 são decrescentes e suas retas formam ângulo entre 90° e 180° com o lado positivo do eixo x.
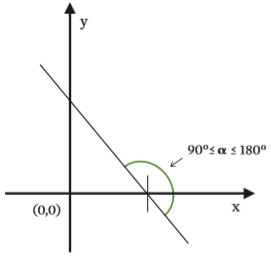
Aliás, lembrando: no plano cartesiano, os ângulos são medidos sempre no sentido anti-horário, a partir do lado positivo do eixo x.
Raiz
O ponto em que uma reta cruza o eixo x se chama raiz da função. Observe que qualquer ponto do eixo x tem coordenada y = 0. Então, para descobrir a raiz de uma função de 1° grau, basta calcular o valor da função para y = 0:

Generalizando: numa função de 1° grau, a raiz é dada pela expressão:
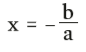
Cruzamento da reta com os eixos
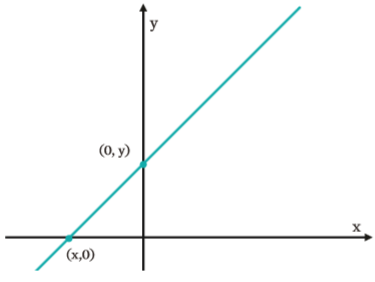
Uma reta inclinada – ou seja, que não seja nem horizontal nem vertical – sempre cruza tanto o eixo x quanto o eixo y. O cruzamento no eixo y se dá no ponto em que x = 0 e terá coordenadas (0, b) – ou seja, x = 0 e b é o coeficiente linear da reta. O cruzamento no eixo x ocorre no ponto de coordenada (x,0). Veja abaixo:
Equação de 1° grau
Toda função é uma igualdade que só pode ser estabelecida se conhecermos as coordenadas de dois pontos da reta por ela definida. Uma equação é também uma igualdade, mas define apenas um dos pontos do gráfico. Veja a diferença com um exemplo:
Qual é o valor de x que torna verdadeira a expressão 2x + 5 = 9?
O primeiro passo e isolar x em um dos lados da expressão:
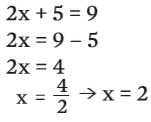
O valor 2 para a incógnita x é a solução da igualdade. Ou seja, o conjunto solução da equação é S = {2}.
Repare que encontramos apenas um par coordenado da reta: (2, 9).
Então, a partir de uma função, quando isolamos a variável x, acabamos criando uma equação.
Análise de sinal
Fazer a análise de sinal de uma função significa determinar os valores de x para os quais y será negativo, e os outros valores para os quais y será positivo. Para isso, o primeiro passo é encontrar o valor no qual y = 0. Acompanhe no exemplo a seguir.

Para analisar o sinal, fazemos um esboço do gráfico da função. Já conhecemos as coordenadas de um dos pontos da reta (3,0). O coeficiente angular é maior que zero (a > 0). Portanto, a reta é crescente e faz um ângulo entre 0° e 90° com o eixo x.
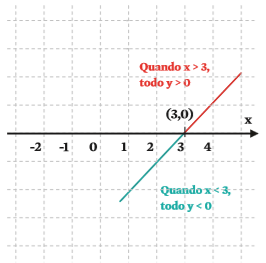
Então, a análise de sinal indica que:
A função é positiva para todo x real maior que 3: f(x) > 0, se x > 3 | x ∈ R
E é negativa para todo x real menor que 3: f(x) < 0, se x < 3 | x ∈ R

SINAIS EM FUNÇÕES E EQUAÇÕES
Não se esqueça: ao isolar uma incógnita em um dos lados de uma equação, você deve inverter a operação dos termos transferidos de lado. O que de um lado é somado, do outro deve ser subtraído; o que é multiplicado deve ser dividido. E vice-versa. Por exemplo:
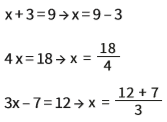
Inequações
Existem expressões matemáticas que, diferentemente do que ocorre com funções e equações, exprimem uma desigualdade. Essas desigualdades são indicadas pelo sinais:
- > (maior que)
- < (menor que)
- ⩾ (maior ou igual a)
- ⩽ (menor ou igual a)
Resolvemos uma inequação de primeiro grau seguindo os mesmos passos usados para a resolução de equações de 1° grau, com uma particularidade importante: em algumas situações o sinal de desigualdade é invertido (veja o Atenção ao lado). Acompanhe no exemplo a seguir.
Que valores de x tornam verdadeira e inequação 3x – 9 ⩾ 0, com x ∈ R.
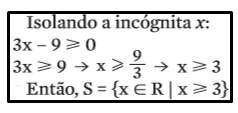
Veja que são infinitas as possibilidades de valores para x a fim de tornar a inequação verdadeira: para qualquer valor igual ou maior que 3, a função dará sempre um resultado maior ou igual a zero.

INVERSÃO DE SINAL
Quando, numa inequação de 1° grau, o coeficiente de x for negativo (x < 0), devemos inverter o sinal de desigualdade: de > ou ≥ para < ou ≤, e vice-versa.
SISTEMA DE EQUAÇÕES
Você deve se lembrar: sistema de equações é uma forma de combinar duas equações, com duas variáveis, que permite definir o valor dessas variáveis que são válidos para ambas. Para resolver um sistema de equações, podemos realizar diversas operações.
- → Subtração: Quando qualquer um dos coeficientes (a ou b) é o mesmo, simplesmente subtraímos uma equação de outra. Veja o exemplo a seguir.
Considere o sistema:
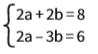
O coeficiente de a é o mesmo em ambas as equações (a = 2). Então podemos simplesmente subtrair uma da outra:
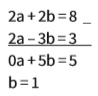
Para encontrar o valor de a, basta substituir o valor de b = 1 em qualquer uma das equações:
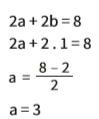
- Multiplicação: Quando as duas equações não têm em comum nenhum coeficiente, nem a, nem b, multiplicamos as equações por um número que iguale um desses coeficientes. Para isso, é preciso encontrar o número certo – o mínimo múltiplo comum (MMC) entre os coeficientes a e b de uma delas. Com um exemplo fica mais fácil entender:Resolva o sistema
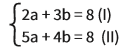
Veja que entre as duas equações, nem o coeficiente de a, nem o de b são iguais. Vamos, encontrar o MMC entre os coeficientes de a das duas equações, 2 e 5. O MMC é 10. Isso significa que, para deixar as duas equações com o mesmo coeficiente, temos de multiplicar a primeira equação por 5 e a segunda por 2:
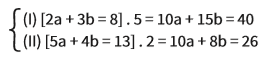
Agora podemos subtrair uma da outra:
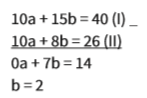
Encontrado b, definimos o valor de a substituindo b em qualquer uma das equações:
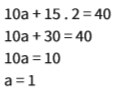
A solução para o sistema é a = 1 e b = 2
Sistemas de equação são úteis para definir pontos em comum em retas concorrentes.
Domínio de uma função
Domínio, em matemática, é o nome que se dá às condições necessárias para que uma função se torne verdadeira. Por exemplo: você sabe que não é possível dividir um número real por zero. Portanto, para que uma função do tipo f(x)= 3/(4 . x), a variável x tem de ser diferente de zero, obrigatoriamente. Mas x pode assumir valores maiores ou menores que zero.
O mesmo é válido para raízes quadradas. Não é possível extrair a raiz quadrada de números negativos. Portanto, para a expressão ![]() jamais poderá dar um número menor que zero. Então x nunca pode assumir valores menores que 4. Repare que quando definimos o domínio de uma função, estamos resolvendo uma inequação.
jamais poderá dar um número menor que zero. Então x nunca pode assumir valores menores que 4. Repare que quando definimos o domínio de uma função, estamos resolvendo uma inequação.

ANÁLISE DE SINAL
Faça a análise de sinal da função -2x + 8 = y Primeiro, encontramos a raiz da função, atribuindo a y o valor 0
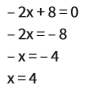
Então a reta passa pelo ponto (4,0).
Identificamos na expressão que o coeficiente a < 0. Portanto, a reta é decrescente e faz um ângulo entre 90° e 180° com o eixo x:
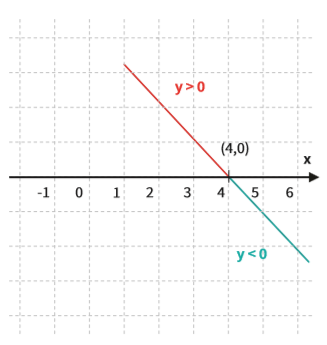
Portanto, sabemos que:
- f(x) > 0 se x < 4
- f(x) < 0 se x > 4
INEQUAÇÕES
Determine o conjunto-solução da inequação: -3x + 6 < 0.
![]()
É fácil constatar que apenas os valores de x maiores que 2 tornam a sentença verdadeira. Basta substituir na inequação qualquer valor menor que 2:
Para x = 1, temos:
![]()
3 não é menor que zero, portanto esse valor não torna a inequação verdadeira.
Mas, se, na mesma expressão, atribuirmos a x qualquer valor maior que 2, confirmamos a inequação.
Para x = 3, temos:
![]()
O valor -3 é menor que zero. A expressão é verdadeira.
DOMÍNIO DE UMA FUNÇÃO
Determine o domínio da função ![]() em que x ∈ R. Não existe raiz quadrada de número negativo. Portanto, para que a expressão acima seja uma função no campo dos números reais, precisamos garantir que o radicando (2x + 3) seja estritamente positivo ou nulo (a raiz quadrada de 0 é 0). Daí temos a inequação 2x + 3 ⩾ 0.
em que x ∈ R. Não existe raiz quadrada de número negativo. Portanto, para que a expressão acima seja uma função no campo dos números reais, precisamos garantir que o radicando (2x + 3) seja estritamente positivo ou nulo (a raiz quadrada de 0 é 0). Daí temos a inequação 2x + 3 ⩾ 0.
Resolvendo a inequação:
![]()
O domínio da função é D = {x ∈ R | x ⩾ -3/2}

(…) Segundo análises de demógrafos e economistas, as três primeiras décadas deste milênio seriam o momento histórico de impulso para o Brasil dar o salto do crescimento econômico e do desenvolvimento social (…) “Este é o momento em que a janela de oportunidade vai estar aberta em sua maior amplitude”, demarca José Eustáquio Diniz Alves, [professor da Escola Nacional de Ciências Estatísticas](…).
(…) “Para aproveitar esse momento de bônus demográfico são necessárias políticas para combater dois problemas que temos hoje entre os jovens. Um associado aos ‘nem-nem’ [jovens que nem estudam, nem trabalham] e outro relacionado à mortalidade”, pondera o economista [Guilherme Diniz Irfi, professor da Universidade Federal do Ceará].
O Povo on-line, 1/2/2015