Cinemática: MRUV (Movimento Retilíneo Uniformemente Variado)

EXPLOSÃO DE VELOCIDADE O guepardo atinge 72 km/h em apenas 2 segundos. Sua aceleração é a mesma de um carro de Fórmula 1

Variação gradual

O movimento retilíneo uniformemente variado, ou MRUV, é o que segue uma trajetória retilínea e apresenta uma alteração uniforme no módulo de velocidade. É um movimento com aceleração diferente de zero e constante – a velocidade do corpo aumenta ou diminui de maneira uniforme ao longo do percurso. 

Módulo: é o valor da intensidade de uma medida. O módulo da velocidade, por exemplo, é um valor em m/s ou km/h. O módulo não indica nem direção nem sentido da velocidade.

O MRUV em que o corpo apresenta um aumento do módulo da velocidade é chamado de movimento acelerado.

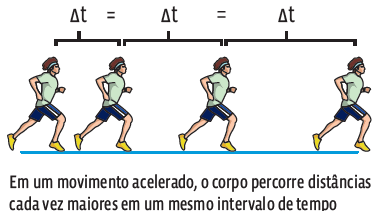
Já o MRUV em que o objeto móvel apresenta diminuição do módulo da velocidade é chamado de movimento retardado.

A aceleração é uma grandeza vetorial – ou seja,para defini-la inteiramente é preciso considerar seu valor (módulo), sua direção e seu sentido.Uma aceleração cujo sentido coincide com o sentido adotado como positivo para a trajetória tem valores positivos (a > 0). No sentido oposto ao sentido adotado como positivo, valores negativos (a < 0).

FUNÇÃO HORÁRIA DA VELOCIDADE

O MRUV é caracterizado pela alteração da velocidade do corpo. A equação que fornece a velocidade do corpo em um instante qualquer é a chamada função horária da velocidade:

v (t) = v₀ + a . t, em que:

-> v(t) é a velocidade do corpo num instante t;

-> v₀ é a velocidade inicial do corpo;

-> a é a aceleração do corpo;

-> t é um instante qualquer.

Se um atleta parte do repouso e acelera uniformemente a 3 m/s², a função horária de sua velocidade é:

v(t) = v₀ + a . t ⇒ v(t) = 0 + 3 . t ⇒ v(t) = 3 . t

Se o atleta consegue manter essa aceleração por 3 segundos, sua velocidade ao final da aceleração é:

v(t) = 3 . t ⇒ v = 3 . 3 ⇒ v = 9m/s

FUNÇÃO HORÁRIA DA POSIÇÃO

Assim como definimos a posição de um corpo em MRU, sem aceleração, podemos também definir a posição de um corpo que executa um MRUV, com aceleração. A função horária da posição é uma equação matemática que fornece a localização do corpo em qualquer instante do movimento:

Com essa equação determinamos a posição S(t) de um corpo que tem posição inicial S₀, velocidade inicial v₀ e aceleração a em qualquer instante t.

Um ciclista parte do repouso na posição inicial 10 m de determinado referencial e acelera 4 metros por segundo a cada segundo. A função horária para sua velocidade é:

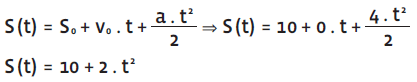
No instante 4 segundos, ele estará no ponto:

Depois de 4 segundos, o ciclista estará na posição 42 m do referencial. Descontados os 10 m de distância entre o referencial e sua posição de partida, ele terá percorrido 32 m.

EQUAÇÃO DE TORRICELLI

Combinando a equação horária da velocidade e a equação horária da posição, encontramos a chamada equação de Torricelli. A equação de Torricelli não considera o tempo de percurso. É útil quando não temos essa informação.

v² = v₀² + 2 . a. ΔS, em que:

-> v é a velocidade final do corpo;
-> v₀ é a velocidade inicial do corpo;
-> a é a aceleração do corpo;
-> ΔS é o deslocamento escalar do corpo.

Um automóvel se desloca a 36 km/h. O motorista avista um sinal vermelho 20 metros à frente e para exatamente no sinal. Qual a aceleração do veículo nessa situação?

Sabemos que:

• A velocidade inicial do automóvel é 36 km/h (ou 10 m/s);
• A velocidade final é zero;
• A distância percorrida até o sinal é de 20 m.

Substituindo os valores na equação de Torricelli:

O sinal negativo indica que a aceleração foi aplicada no sentido inverso ao adotado como positivo: o módulo da velocidade do automóvel diminui 2,5 m/s a cada segundo.

GRÁFICOS DO MRUV

Um MRUV também pode ser representado em gráficos.

Aceleração em função do tempo

A velocidade varia, mas a aceleração se mantém igual durante o tempo do percurso. Então, esse gráfico é uma reta paralela ao eixo do tempo. Um MRUV cuja aceleração tem o mesmo sentido do que foi adotado como positivo a presenta a > 0:

Já um MRUV cuja aceleração tem sentido oposto ao que foi adotado como positivo apresenta a < 0. Então, a reta que representa a aceleração sai de um ponto abaixo do zero:

Velocidade em função do tempo

A velocidade de um corpo em MRUV varia com o tempo de acordo com a função horária da velocidade:

v (t) = v₀ + a . t

Esta é uma equação de 1º grau cujo gráfico é uma reta. Neste caso, o coeficiente linear fornece a velocidade inicial do corpo (v₀) e o coeficiente angular, a aceleração (a).

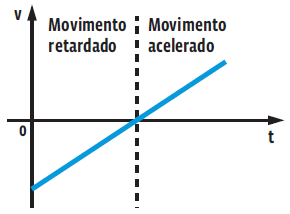
Para o caso de um MRUV com aceleração positiva (a > 0), a função é crescente e o gráfico da velocidade em função do tempo tem o seguinte formato:

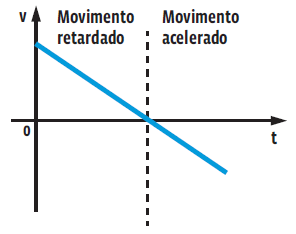
Para o caso de um MRUV com aceleração negativa (a < 0), a função é decrescente e o gráfico da velocidade em função do tempo tem o seguinte formato:

O gráfico da velocidade em função do tempo também fornece o deslocamento escalar executado pelo corpo. Veja a seguir:

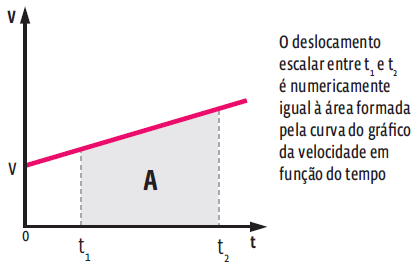
Posição em função do tempo

A posição de um corpo em MRUV varia como tempo de acordo com o que chamamos de função horária da posição:

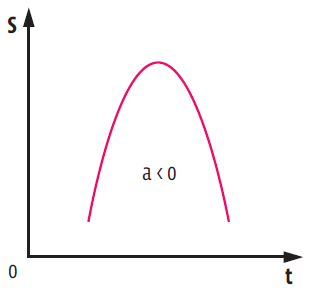
Esta é uma equação de 2º grau e, portanto, define uma parábola como gráfico. O sinal do coeficiente do termo quadrático da equação (termo que acompanha t²) indica se a aceleração é maior ou menor que zero. E isso pode ser descoberto pela concavidade da parábola.

Um MRUV com aceleração positiva (a > 0) resulta numa parábola com concavidade voltada para cima:

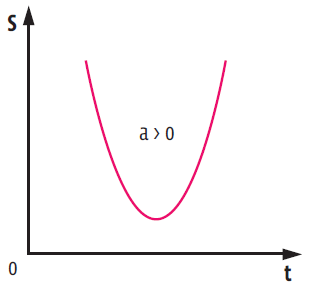
Já para um MRUV com aceleração negativa(a < 0), a parábola do gráfico tem concavidade voltada para baixo:

Num movimento acelerado:

• velocidade e aceleração têm mesmo sinal;
• o módulo da velocidade aumenta no decorrer do tempo.

Num movimento retardado:

• velocidade e aceleração têm sinais opostos;
• o módulo da velocidade diminui no decorrer do tempo.

Toda função de 2º grau (ax² + bx + c) tem como gráfico uma parábola. A concavidade da parábola é dada pelo sinal do coeficiente de x².

• Para a > 0, a concavidade é para cima.
• Para a < 0, a concavidade é para baixo.