Geometria: Ponto, reta e plano
Os elementos essenciais das figuras geométricas lineares

O REAL ACHATADO O plano, como o do papel em que o desenho ao lado é feito, admite apenas figuras de duas dimensões
Só duas dimensões
Retas e ângulos são os elementos essenciais das figuras geométricas lineares
Geometria é a área da matemática que estuda o espaço e as figuras que ocupam esse espaço – suas formas, suas dimensões e as relações que podem ser estabelecidas entre elas. O espaço estudado pela geometria pode ser plano ou tridimensional.
Plano, ponto e reta
Plano é definido como um objeto geométrico que tem apenas duas dimensões: comprimento e largura. O elemento mais simples de um plano é o ponto, uma entidade que não tem dimensões. Bastam três pontos para definir um plano.
O segundo elemento mais simples é a reta – um conjunto de infinitos pontos, enfileirados, sempre em uma mesma direção e nos dois sentidos. Ou seja, qualquer reta tem comprimento infinito, mas não tem largura. Para definir uma reta precisamos de apenas dois pontos.
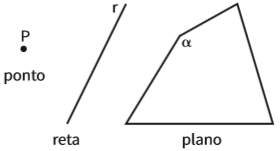
Os geômetras adotam algumas convenções, que você deve conhecer:
- pontos são normalmente batizados com letras maiúsculas: A, B, C, O…;
- retas são geralmente indicadas por letras minúsculas: r, t, s…;
- e planos costumam ser indicados por letras do alfabeto grego: α (alfa), β (beta) e γ (gama).
Posições da reta em relação ao plano
Uma reta pertence a um plano se pelo menos dois de seus pontos pertencerem a esse plano.
Se isso acontecer, então todos os outros pontos da reta também pertencerão ao plano. Veja:

A e B ∈ r; A e B ∈ α → r ∈ α Ou seja, a reta r está contida no plano α.
Uma reta pode ser paralela a um plano. Nesse caso, nenhum de seus pontos pertence ao plano: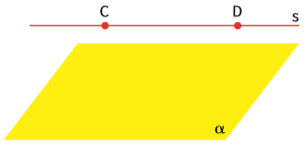
C e D ∈ s; C e D ∉ α → s ∉ α. Portanto, a reta s é paralela a α.
Uma reta pode, finalmente, cortar o plano em um ponto qualquer.
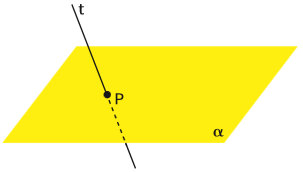
t ∩ α = P → t é secante ao plano.
Posição relativa de retas
Pensando na reta como um conjunto de pontos e usando a linguagem dos conjuntos, fazemos relações entre elas.
Duas retas que ocupam um mesmo plano podem ser:
• Paralelas: não têm ponto em comum.

Lembrando que toda reta é infinita, se duas retas não forem paralelas, elas se cruzarão em algum lugar. Inversamente, se a intersecção do conjunto de pontos da reta r com o conjunto de pontos da reta s for um conjunto vazio, as retas são obrigatoriamente paralelas:
r // s ↔ r ∩ s = Ø∙
O sinal ↔ indica que a recíproca é verdadeira.
• Concorrentes: são retas que se cruzam e têm um único ponto em comum.
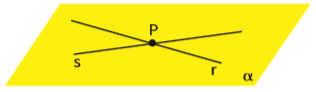
Duas retas quaisquer r e s são concorrentes quando a intersecção entre os conjuntos de pontos de cada uma delas resulta num conjunto de um único ponto: r ∩ s = {P}.
Ângulos
Quando duas semirretas (trechos de uma reta) têm origem em um mesmo ponto e seguem direções diferentes, elas dividem o plano em duas regiões chamadas ângulos. O ponto de origem das semirretas é denominado vértice dos ângulos (O). Os ângulos, como os planos, também costumam ser representados por letras do alfabeto grego.
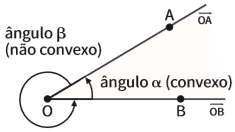
Duas retas que se cruzam dividem o plano em quatro regiões distintas, ou seja, em quatro ângulos. Veja:
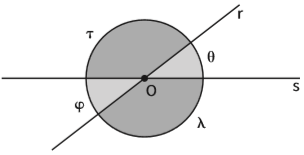
Os ângulos λ e τ são opostos pelo vértice; θ e φ também são opostos pelo vértice. Ângulos opostos pelo vértice são congruentes (têm a mesma medida).
Retas perpendiculares são retas concorrentes que se cruzam formando quatro ângulos congruentes, cada um deles medindo 90° (ângulo reto).
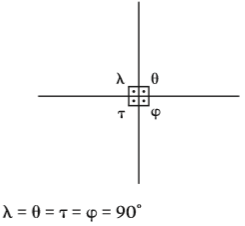
Transversal e paralelas
Duas retas paralelas que são cortadas por uma terceira reta (transversal) formam oito ângulos que se relacionam de maneira bem específica. Acompanhe na figura as explicações no texto a seguir
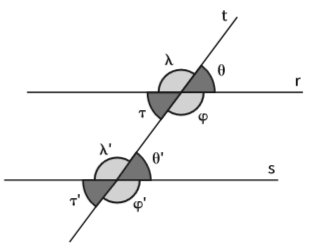
- • Ângulos adjacentes são ângulos que compartilham um mesmo lado:
Entre as retas r e t, são adjacentes os pares λ/θ, τ/λ, τ/φ e φ/ θ;
Entre as reta s e t, são adjacentes os pares λ’/θ’, τ’/λ’, τ’/φ’ e φ’/θ’.
Os ângulos adjacentes somam 180º – ou seja, formam um conjunto de ângulos suplementares.
- • Ângulos opostos pelo vértice como já vimos, são ângulos que compartilham o vértice, mas não compartilham lados. Dois ângulos opostos pelo vértice são sempre congruentes. No caso das duas paralelas cortadas por uma transversal, são opostos pelo vértice os pares λ/φ, θ/ τ, λ’/φ’ e θ’/τ’.
- • Ângulos alternos são pares de ângulos que estão em lados diferentes (alternados) da reta transversal. Dois ângulos alternos têm medidas iguais. Os alternos são internos quando ficam entre as retas paralelas. Na figura, são alternos internos os pares τ/θ’ e λ’/φ.
Ângulos alternos externos são aqueles que estão na região externa das retas paralelas (acima ou abaixo delas). São alternos externos os ângulos λ/φ’ e θ/τ’.
- • Ângulos colaterais são aqueles que ocupam o mesmo lado da reta transversal. Eles também podem ser internos (entre as paralelas) ou externos. Na figura, são colaterais internos τ/λ’ e φ/θ’; são colaterais externos λ/τ’e θ/φ’.
- • Ângulos correspondentes são aqueles que se encontram do mesmo lado da reta transversal, um na região interna das retas paralelas e outro na região externa. Ângulos correspondentes são congruentes. Na figura, são pares de ângulos correspondentes λ/λ’, τ/τ’, θ/θ‘ e φ/φ’.
PARALELAS E TRANSVERSAIS
Observe a figura abaixo.
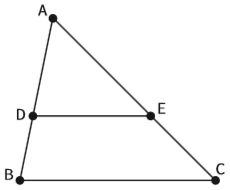
Repare que existem aqui dois triângulos (ABC e ADE). E que os lados DE e BC são paralelos. O que se pode dizer sobre os valores dos ângulos de vértices em B, C, D e E?
Por partes:
• Se você prolongar as retas dos segmentos BC, DE, AB e AC, vai reconhecer a situação como a de duas retas paralelas (DE e BC) cortadas por duas transversais (AB e AC). Veja:
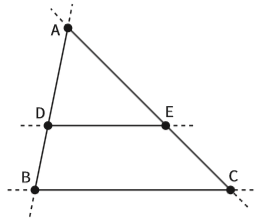
• Em relação à transversal AC, os ângulos com vértices em C e E são correspondentes e, portanto, congruentes. O mesmo ocorre com os ângulos D e B, em relação à transversal AB. Esta situação é muito importante para reconhecer a semelhança entre triângulos.
Mais importante que conhecer os nomes desses pares de ângulos é saber reconhecer as relações entre eles. E, para isso, você só precisa treinar a observação – reparar as semelhanças e diferenças entre dois ângulos.
Teorema de Tales
Retas transversais mantêm uma relação de proporção bem definida. E o que define essa proporção é o teorema de Tales: qualquer conjunto de retas paralelas cortadas por segmentos transversais formam nessas transversais segmentos proporcionalmente correspondentes. Mais fácil acompanhando na figura:
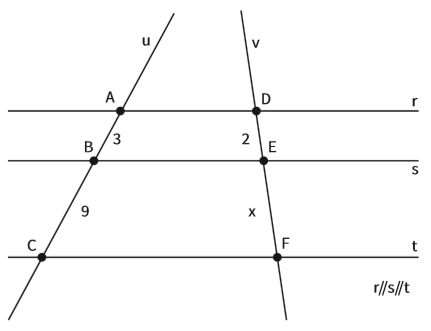
Veja:
• As retas r, s e t formam um feixe de retas paralelas;
• As retas u e v (que não são paralelas, mas concorrentes) cortam o feixe r, s e t. Os pontos de intersecção das três retas definem os pontos A, B, C, D, E e F.
Segundo Tales, os segmentos correspondentes em cada uma das retas transversais são proporcionais. Na figura, as medidas de AB e DE guardam uma razão de 3/2. Então, os segmentos BC e EF têm a mesma relação de proporção. Ou seja,

Teorema de Tales
Qual a medida do segmento DF, na figura abaixo?
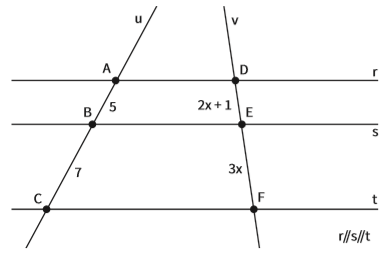
Por Tales, sabemos que AB/DE = BC/EF. Então,
![]()
Multiplicando em cruz:
5 . 3x = 7 . (2x + 1)
15x = 14x + 7
x = 7
O segmento DE = 2 . x + 1 = 2 . 7 + 1 → DE = 15
O segmento EF = 3 . x = 3 . 7 → EF = 21
Por fim, o segmento DF é a soma de DE e EF: 21 + 15 → DF = 36

QUANDO TALES NÃO RESOLVE
Para resolver um problema de retas paralelas e transversais, só podemos usar o teorema de Tales quando temos as medidas de todos os segmentos de uma das retas que não são paralelas. Caso contrário, não é possível aplicar o teorema de Tales. Veja a figura:
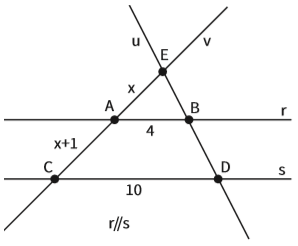
Não temos a medida de nenhum dos segmentos da reta u. Mas temos as medidas de dois lados de dois triângulos:
• Do triângulo AEB, conhecemos os lados AB = 4 e AE = x;
• Do triângulo CED, conhecemos os lados CD = 10 e CE = x + 1 + x ;
• Esses dois triângulos compartilham o ângulo no vértice E. Os ângulos em A e C são congruentes. O mesmo ocorre entre os ângulos em B e D. Portanto os dois triângulos são semelhantes. Nesse caso, usamos semelhança de triângulos.










