Álgebra: Posições relativas de retas
AO INFINITO E ALÉM. Retas paralelas, como trilhos de trem na foto acima, se vistas num plano cartesiano, mantêm relações especiais.
Paralelas, concorrentes ou perpendiculares
As funções que definem as relações entre retas em um mesmo plano
Duas retas distintas e que ocupem um mesmo plano apresentam, uma em relação à outra, diferentes posições. Elas podem ser paralelas, concorrentes ou perpendiculares. E, em cada um desses casos, as retas mantêm entre si algumas relações algébricas.
Paralelas
São duas retas em um mesmo plano que jamais se encontram – portanto, não têm ponto em comum. Para que isso aconteça, as duas retas devem fazer, com a horizontal, ângulos de mesmo valor. Sabemos que o coeficiente angular da forma geral da equação da reta está diretamente ligado à sua declividade – ou seja, a esse ângulo com a horizontal. Então, para duas retas serem paralelas, elas devem ter a mesma declividade, ou seja, o mesmo coeficiente a. Veja:
As retas abaixo são definidas por duas equações diferentes:
Repare que, nas duas equações, o coeficiente angular a tem o mesmo valor: 2. Portanto, são paralelas, independentemente do coeficiente b (coeficiente linear). Conhecendo a equação de uma reta, descobrimos a equação de qualquer paralela a ela, desde que saibamos um ponto pelo qual essa segunda reta passa. Acompanhe no exemplo a seguir.
Encontre a equação da reta r que passa pelo ponto Pr (2, 3) e que é paralela à reta s, cuja equação é y = (1/2x) + 5.
A forma geral da equação de qualquer reta é y = a . x + b.
Duas retas paralelas têm o mesmo coeficiente a. Conhecemos esse coeficiente da equação da reta s. Então ar = as = 1/2
Não conhecemos o valor de b para a reta s. Mas temos os valores de x e y, nas coordenadas do ponto PR (2,3) → x = 2 e y = 3.
Para descobrir o valor de b da reta r, basta substituir todos esses valores (a, x e y) na forma geral da equação:
y = a . x + b
3 = 1/2 . 2 + b → 3 – 1 = b → b = 2
Portanto, a equação da reta r é 
Para desenhar as duas retas, definimos dois pontos de cada reta, atribuindo diferentes valores para x e encontrando os valores correspondente de y.
Para a reta r: conhecemos o ponto Pr (2,3). Para encontrar o segundo ponto, lembramos da raiz da equação: o ponto em que a reta cruza o eixo x. Nesse ponto, y vale zero.
Então, pela equação de
sabemos que
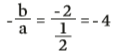
Portanto, outro ponto de r é Pr (-4, 0).
- Para a reta s: não conhecemos nenhum ponto. Mas temos a equação geral: y = 1/2x + 5. O valor de x na raiz é dado por
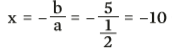Um dos pontos dessa reta, então é Ps (0, -10). - Para encontrar um segundo ponto de s, definimos o valor de y quando x = 0, substituindo esses valores na equação da reta
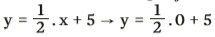
O segundo ponto de s, então, é (0,5). No gráfico:
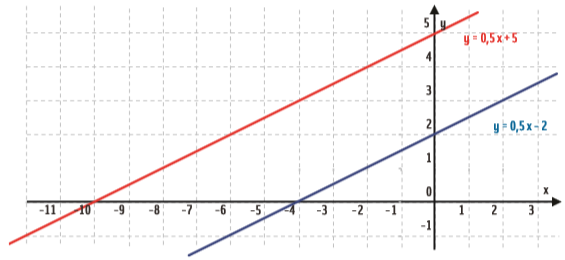
Concorrentes
São retas num mesmo plano que apresentam um ponto em comum. Isso sempre acontecerá quando as retas tiverem declividades diferentes. E as coordenadas do ponto em comum satisfazem as duas equações. Acompanhe no exemplo.
Quais as coordenadas do ponto de encontro das retas de equações (I) y = 2 . x – 5 e (II) y = -3 . x + 10?
A questão pede que encontremos as coordenadas do ponto P(x,y) que sejam válidas para as duas equações. Então, podemos estabelecer a igualdade entre as equações nesse ponto:
2 . x – 5 = -3 . x + 10
5x = 15 → x = 3
Para encontrar a coordenada y, basta substituir esse valor em qualquer uma das equações: y = 2 . 3 – 5 → y = 1. Repare que chegaríamos ao mesmo resultado trabalhando com a segunda equação: y = -3 . 3 + 10 = 1. Outra maneira de resolver este problema é com um sistema de equações
Perpendiculares
As retas perpendiculares também são concorrentes, mas têm algumas características especiais. Duas perpendiculares se cruzam em ângulo reto (90°). E, para que isso ocorra, o coeficiente angular de uma das retas deve ser o inverso do oposto do outro.
Veja duas retas perpendiculares, representadas no plano cartesiano, com suas respectivas equações:
PERPENDICULARES
Determine a equação da reta que seja perpendicular à reta definida pela função f(x) = – 3x + 2 e que passe pelo ponto (6, 1).
Vamos chamar a função da reta que se pede de g(x). Se as duas retas são perpendiculares, o coeficiente de x de uma deve ser o inverso do oposto do coeficiente da outra. Em f(x) = -3x + 2, o coeficiente de x = -3.
Portanto, em g(x), o coeficiente de x é 1/3
Como para qualquer reta, a equação tem este formato: g(x) = ax + b.
Conhecemos o coeficiente a. E temos as coordenadas de um ponto dessa reta: (6,1). Vamos substituir tudo na expressão de g(x):
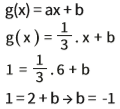
A equação da reta perpendicular a f(x) pelo ponto (6, 1) é:
