Potência e Logaritmo: Funções e equações logarítmicas


RABISCOS DE UM TERREMOTO. As ondas de um tremor são registradas por um sismógrafo. A escala Richter, que mede a intensidade do abalo, é logarítmica
Para medidas extremas
Como os logaritmos permitem comparar valores que variam muito
Você já viu no início deste capítulo: a energia liberada por um terremoto se propaga em ondas[1]. Os sismógrafos captam essas ondas e indicam a amplitude delas. Quanto maior a amplitude, maior a energia liberada e, portanto, maior a intensidade do tremor. A medida dessa intensidade é dada pela escala Richter como magnitude.
A cada ponto da escala, a energia liberada aumenta 31,6 vezes. A energia de um tremor de 5 pontos na escala Richter é igual àquela liberada pela explosão de 32 toneladas de dina- mite. Outro abalo, de magnitude 6, libera uma energia equivalente a 1 milhão de toneladas de explosivos. Essa diferença é tão grande porque a escala Richter é uma escala logarítmica.
Ondas – O QUE ISSO TEM A VER COM FÍSICA?
Onda é um fenômeno estudado pela física. Uma onda só transfere energia cinética para o meio, jamais carrega matéria. Existem ondas mecânicas – como as que se propagam na água quando se lança uma pedra – e ondas eletromagnéticas, como as da luz.
Definição de logaritmo
O logaritmo de um número é a operação para encontrar o expoente de uma potência. Veja:
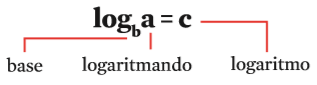
Existem algumas condições para que um logaritmo exista:
![]()
Uma das vantagens de compreender a relação entre logaritmo e potência é que, se você estiver trabalhando com vários valores, todos dados na forma de potências de mesma base, pode deixar a base de lado e operar somente com os expoentes. Por exemplo:
Imagine um problema que exija que se multipliquem os números:
100
10 000
0,00001
1 000 000 000 000
0,01
Repare que todos os valores apresentados são potências de 10:
100 = 102
10 000 = 104
0,00001 = 10-5
1 000 000 000 000 = 1012
0,01 = 10-2
Para multiplicar esses valores, basta manter a base 10 e somar os expoentes:
2 + 4 – 5 + 12 – 2 = 11
O resultado é 1011
Seguindo o mesmo raciocínio, a divisão desses números pode ser feita simplesmente subtraindo-se os expoentes:
100 : 10 000 : 0,00001 : 1 000 000 000 000 : 0,01 =
102 : 104 : 10-5 : 1012 : 10-2
Trabalhando com os expoentes, temos:
2 – 4 – (–5) – 12 – (–2) = –7
O resultado será 10–7
Propriedades dos logaritmos
As propriedades dos logaritmos são direta- mente obtidas das propriedades das potências.
Vamos considerar, nos exemplos a seguir, a sequência formada pelas potências de base 2:
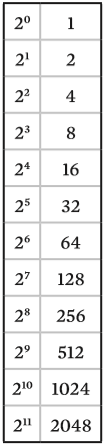
Em primeiro lugar, vamos simplesmente aplicar a definição de logaritmo para determinar alguns deles. Assim:
![]()
Ora, se 25 = 32, então, pela definição, log2 32 = 5
Assim, também podemos dizer que:
log2 256 = 8, pois 28 = 256.
log2 1 = 0, pois 20 = 1.
Logaritmo do produto
Qual é o logaritmo em base 2 do produto de 16 por 64? O que se pede é o expoente a que devemos elevar 2 para obter o produto indicado. Em linguagem matemática:
log2(16 . 64) = log2 1 024
Sabemos que:
• 16 = 24
• 64 = 26
Então, 1 024 = 24 . 26
Pela propriedade das potências, para multi- plicar potências de mesma base, basta somar os expoentes. Então, 1 024 = 210
Portanto, log2 1 024 = 10
Podemos generalizar:
logb (a . c) = logb a + logb c
No sentido inverso, a soma de logaritmos de mesma base é o logaritmo do produto dos logaritmandos:
logb a + logb c = logb (a . c)

LOGARITMO DE PRODUTO
Resolva a operação log2 (8 . 32).
Pela propriedade do logaritmo de produto,
log2 (8 . 32) = log2 8 + log2 32
• O expoente a que 2 deve ser elevado para se chegar a 8 é 3, pois 8 = 2 . 2 . 2.
Então, log2 8 = 3.
• E o expoente a que 2 deve ser elevado para se chegar a 32 é 5, pois 32 = 2 . 2 . 2 . 2 . 2.
Portanto, log2 32 = 5.
Então, log2 (8 . 32) = log2 256 = 3 + 5 = 8
O expoente a que 2 deve ser elevado para se chegar a 256 é 8: 28 = 256
Logaritmo do quociente
Na divisão de potências de mesma base, o que fazemos com os expoentes é subtraí-los, certo? A mesma regra é válida para logaritmos. Acompanhe o exemplo:
Se quisermos fazer a divisão 512 por 4, podemos tomar os logaritmos na base 2 para 512 (9) e de 4 (2) e subtraí-los (9 – 2 = 7). Assim, o resultado de
![]()
Generalizamos em:
![]()
No sentido inverso, a subtração de dois logaritmos de mesma base é o quociente dos logaritmandos:
![]()

LOGARITMO DE QUOCIENTE
Qual o resultado da operação:
![]()
Pela propriedade de logaritmo do quociente, temos:
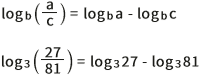
• O expoente a que 3 deve ser elevado para chegarmos a 27 é 3, pois 27 = 3 . 3 . 3
Então, log3 27 = 3
• Já o expoente a que 3 deve ser elevado para chegarmos a 81 é 4, pois 81 = 3 . 3 . 3 . 3.
Então, log3 81 = 4.
Portanto:
![]()
O expoente a que 3 deve ser elevado para conseguirmos o valor 27/81 é – 1:
![]()
Logaritmo de potência
Vamos partir de logb a = c
Se quisermos saber quanto vale logb an, podemos fazer, por conta da propriedade do produto de potências:
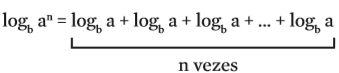
Temos então:
![]()
Ou:
![]()
Quando o logaritmo e a potência têm a mesma base, o logaritmo é o expoente da potência:
![]()
Fácil de entender: na expressão acima, a é o número de vezes que b deve ser multiplicado por si mesmo (o expoente de uma potência de b), para que se obtenha o resultado a. Ora, como ba = ba, a resposta é a vezes.

LOGARITMO DE POTÊNCIA
Qual o valor de log7 2 401?
A primeira coisa a fazer é decompor 2 401 em números primos, pela fatoração. Basta dividir esse valor, seguidas vezes, por seus divisores que sejam números primos, em ordem crescente a começar do 2. Neste caso, o primeiro número primo que é divisor de 2 401 é 7. Então,
Os números, para os dois lados da fatoração:

Portanto, 2 401 = 7 . 7 . 7 . 7 = 74
Faça a operação log7 74
Pela propriedade de logaritmo de potência, temos:
logb na = n . logb a
log7 74 = 4 . log7 7
log7 7 = 1 (ou seja, o expoente a que 7 deve ser elevado para resultar em 7 é 1: 7 = 71
Então, nossa operação fica assim:
log7 74 = 4 . 1 = 4,
pois 2 401 = 74

Sempre que aparecer uma expressão de logaritmo em que a base não é escrita, considere que a base é 10. Assim:
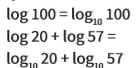
Mudança de base
A partir de um conjunto de valores de logaritmos de certa base, podemos determinar os logaritmos de qualquer número em qualquer outra base.
Na Antiguidade, vários matemáticos se preocuparam em obter uma tabela de logaritmos em base 10. Imagine que tenhamos acesso a uma dessas tabelas e queiramos calcular o logaritmo de 2 na base 3, a partir dos logaritmos de 2 e de 3 na base 10.
São dados:
log 2 = x
log 3 = y
Queremos calcular o valor de m:
log32 = m
Dos dados, concluímos que
10x = 2 e 10y = 3
Queremos determinar m, tal que 3m = 2
Podemos substituir nessa última equação 3 e 2 por suas potências equivalentes em base 10.
Assim:
(10y)m = 10x 10y . m = 10x
Temos que y . m = x
Então:
![]()
Assim, podemos generalizar:
![]()

MUDANÇA DE BASE
Calcule o log9 81, mudando a base do logaritmo.
Lembrando da fórmula:
![]()
Vamos aproveitar que a base 9 e o logaritmando 81 são potências de 3. Então, temos:
![]()
• O expoente para elevar 3 a 81 é 4;
• O expoente de 3 para se chegar a 9 é 2.
Portanto, temos:
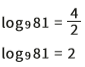
Fácil constatar que a resposta é verdadeira: 92 = 9 . 9 = 81

Não se preocupe: você não precisa saber de cor o valor dos logaritmos de todos os números. Valores quebrados são fornecidos no enunciado das questões da prova.

A ESCALA RICHTER
Usada pela primeira vez pelo físico norte-americano Charles Richter, em 1935, a escala Richter é logarítmica – cada grau é uma potência de base 10. Ou seja, de um grau a outro, a amplitude das ondas sísmicas cresce dez vezes.
Para comparar a diferença na magnitude de dois tremores, fazemos:
M1 – M2 = log A1 – log A2 , em que:
M1 = magnitude do terremoto 1
M2 = magnitude do terremoto 2
A1 = amplitude das ondas do terremoto 1
A2 = amplitude das ondas do terremoto 2
Aplicando a propriedade de subtração de logaritmos:
![]() , Temos:
, Temos:
![]()
A diferença de amplitude das ondas de um tremor de 5 pontos e de outro de 9 pontos na escala Richter:
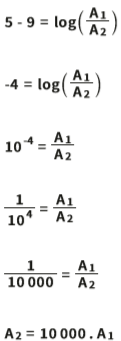
Isso significa que um tremor de 9 graus na escala Richter libera ondas de amplitude 10 000 vezes maior que um tremor de 5 graus.
Função logarítmica
Função logarítmica é aquela que tem como forma f(x) = loga x, com a ≠ 1 e a > 0.
O domínio (D) de qualquer função logarítmica (as condições obrigatórias para que a função tenha solução) é o conjunto de números reais maiores que zero.

DOMÍNIO
Qual o domínio da função (fx) = log (x – 1) 4 – x?
Nesta função, a = x – 1.
Para que f(x) seja função, temos de atender às duas condições:
• 4 – x > 0 → – x > – 4 → x < 4
• x – 1 > 0 → x > 1
• x – 1 ≠ 1 → x ≠ 1 + 1 → x ≠ 2
O domínio é a intersecção dos dois conjuntos definidos por três três condições: x é um número
• real maior que 1
• mas menor que 4
• e diferente de 2.
Em linguagem matemática, D = { x ∈ R | 1 < x < 2 e 2 < x < 4}
Repare que, para definir x ≠ 2, isolamos o 2 em duas desigualdades (x menor que 2 e x maior que 2).

O logaritmo natural (ln) de um número é o logaritmo que tem como base o número de Euler (e ≈ 2,71828…). Este é um número irracional – um número real que não pode ser obtido da divisão de dois inteiros. O número de Euler (e) é também transcendental – não é raiz de nenhuma equação de coeficiente inteiro. O logaritmo natural obedece às propriedades operatórias dos logaritmos em geral. Assim, para resolver questões que trazem ln, basta usar os mesmos processos adotados para logaritmos de bases mais fáceis de lidar, como 2 ou 10.
Gráfico de funções logarítmicas
Vamos comparar os gráficos de duas funções:
y = log2 x
y = log1/2 x
Repare que y corresponde a c (valor do logaritmo), 2 é a base b e x é o logaritmando a.
Atribuindo alguns valores à variável x, calculamos seus logaritmos na base 2 e na base 1/2, completando as tabelas abaixo:
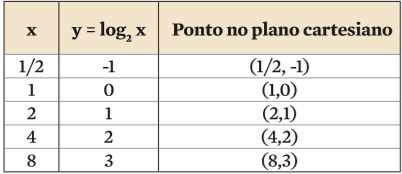
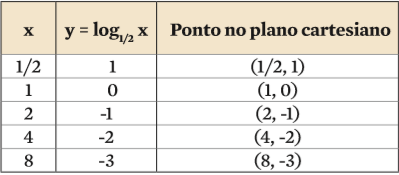
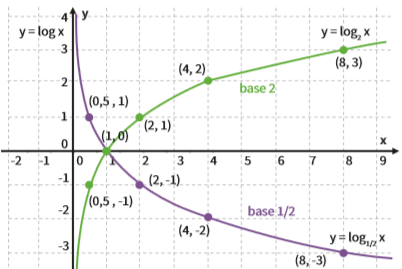
Comparando as duas curvas:
• Repare que em ambas, para todos os pontos, x > 0 e x ≠ 0. Isso está de acordo com o do- mínio das funções logarítmicas.
•S e x nunca é igual nem menor que zero, então as curvas se aproximam do eixo y sem jamais tocá-lo; •A s curvas têm diferentes orientações: para y = log2x, em que a base é maior que 1, a curva é crescente; já para y = log1/2 xb < 1, em que a base é menor que 1, a curva é decrescente.
•A s duas curvas se interceptam no ponto (1,0) que está presente nas duas curvas; isso porque o logaritmo de 1, em qualquer base, é zero.
Equações logarítmicas
São equações em que a incógnita está na base de um logaritmo ou em seu logaritmando. Veja nos dois exemplos:
Em log3 (5x + 1) = 4 , x está no logaritmando;
Em logx (5x + 1) = 4, x é a base do logaritmo.

EQUAÇÃO LOGARÍTMICA
Resolva a equação: log3(5x +1) = 4
Primeiro, vamos estabelecer o domínio dessa equação:
![]()
Aplicando-se a definição de logaritmo temos que:
34 = 81 = 5x + 1
5x = 80
x = 16
Como ![]() , a condição de existência está satisfeita, então S = {16}.
, a condição de existência está satisfeita, então S = {16}.

COM LOGARITMOS DOS DOIS LADOS
A equação pode ter logaritmos dos dois lados da igualdade. Veja:
![]()
Como condição de existência de cada um dos logaritmos, temos:
![]()
Juntando as duas condições, temos que a equação só terá solução se o valor que obtivermos for maior que -2 e menor que 3: -2 < x < 3
Como os dois logaritmos já estão na mesma base (5), igualamos os logaritmandos:
-x + 3 = x + 2
-2x = -1
x = ½
O valor obtido atende às duas condições de existência. Então, S = {1/2}.

ENVOLVENDO EQUAÇÃO DE 2º GRAU
Uma equação logarítmica pode, ainda, envolver equações de segundo grau. Acompanhe:
Resolva: ![]()
Os logaritmos têm a mesma base (2). Então podemos aplicar a propriedade de log do quociente:
![]()
Multiplicando em cruz:
![]()
Resolvendo essa equação de 2º grau, obtemos as raízes
x1 = –1 e x2 = 3.
Agora vamos verificar se x1 e x2 pertencem ao conjunto domínio, voltando à equação inicial:
log2(x2 + 2x –7) – log2(x – 1) = 2
Para x1 = –1, temos:
log2 [(-1)2 + 2(–1) – 7] – log2 [(–1) – 1] =
log2 (-8) – log2 (–2)
Veja que obtemos logaritmos de números negativos, que não existem. Portanto, o valor x1 = –1 não entra no conjunto-solução.
Para x2 = 3, ficamos com
log2(32 + 2 . 3 – 7) – log2(3 – 1) =
log2(8) – log2(2) = 3 – 1 = 2
Os logaritmandos são positivos e encontram-se no conjunto domínio. Então, S = {3}, ou seja, x = 3.

NOVO TERREMOTO NO NEPAL É REAÇÃO AO SISMO DE ABRIL E OUTROS PODEM VIR, ALERTAM ESPECIALISTAS
Semanas após o terremoto de 7,9 graus que matou pelo menos 8 100 pessoas, o novo sismo no Nepal pode ter sido uma reação, e outros tão fortes quanto o de terça-feira ainda poderiam vir. Pelo menos nove réplicas, de até 6,3 graus, foram detectadas até agora (…)
Os terremotos na região se originam com o avanço da placa tectônica da Índia contra a Euroasiática, que geralmente se unem cinco centímetros por ano. O novo tremor teve epicentro na região de Gorkha, perto do Everest, uma das mais afetadas pelo terremoto de abril.
“A falha se deslizou em cerca de uns cinco metros após o terremoto. Como toda a frente da cadeia montanhosa converge, as áreas adjacentes também estão sujeitas a se romper em futuros terremotos (…)”, avaliou Pablo González, especialista da Universidade Leeds.
Extra on-line, 12/5/2015