Dinâmica: Segunda lei de Newton

Devagar com aceleração. Nem sempre um objeto sob aceleração é veloz. Até uma tartaruga sofre aceleração quando muda de direção.
Regras do movimento
Recordando o que foi visto na aula 1 deste capítulo: a primeira lei de Newton, ou princípio da inércia, garante que, se a força resultante que atua sobre um corpo é nula, então esse corpo tem a tendência de permanecer em seu estado de equilíbrio: equilíbrio estático (em repouso) ou equilíbrio dinâmico (em movimento retilíneo uniforme).
Mas o que acontece quando a força resultante que atua em determinado corpo não for nula? Isaac Newton também pensou nisso. E divulgou suas conclusões em sua segunda lei.
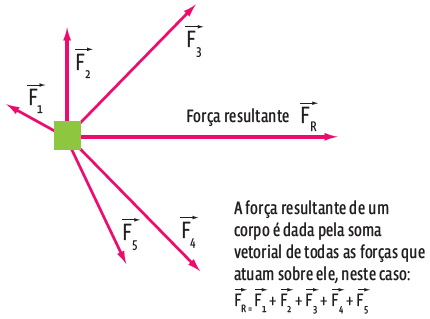
A segunda lei de Newton, ou princípio fundamental da dinâmica, afirma que:
“A aceleração que um corpo adquire é diretamente proporcional à resultante das forças que atuam sobre ele e tem a mesma direção e o mesmo sentido dessa resultante”.
Detalhando: uma força resultante não nula provoca uma aceleração no corpo. E a intensidade dessa aceleração é diretamente proporcional à intensidade da força.
Além disso, a força resultante que atua sobre um corpo e a aceleração causada por essa força têm a mesma direção e o mesmo sentido. Esta é a expressão matemática da segunda lei:
![]()
→ ![]() é a força resultante que atua sobre o corpo, medida em newton (N), no S.I.;
é a força resultante que atua sobre o corpo, medida em newton (N), no S.I.;
→ m é a massa do corpo, medida em kg, no S.I.;
→ ![]() é a aceleração adquirida pelo corpo, cuja intensidade é medida em m/s2, no S.I .
é a aceleração adquirida pelo corpo, cuja intensidade é medida em m/s2, no S.I .

Um newton é a força resultante capaz de dar a um corpo de 1 kg de massa uma aceleração de 1 m/s2
Portanto, a força resultante ( ![]() ) e a aceleração (
) e a aceleração ( ![]() ) são duas grandezas físicas intimamente associadas. E a resultante das forças aplicadas sobre um corpo é igual ao produto de sua massa pela aceleração que o corpo adquire.
) são duas grandezas físicas intimamente associadas. E a resultante das forças aplicadas sobre um corpo é igual ao produto de sua massa pela aceleração que o corpo adquire.
Quanto maior for a intensidade da força resultante aplicada sobre um corpo, maior será a aceleração adquirida:
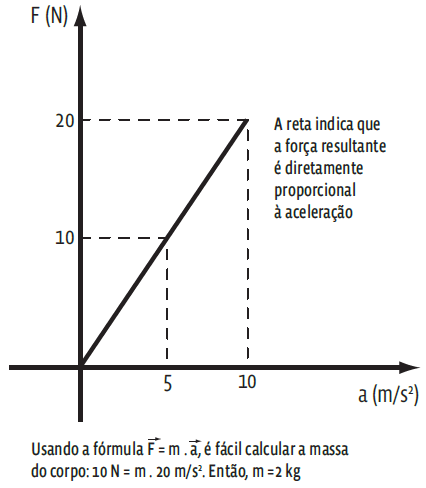
Intuitivamente sabemos que, para produzir a mesma aceleração em uma bicicleta e em um caminhão, são necessárias forças de intensidade bem diferentes. Quanto maior for a massa de um corpo, maior será a força resultante necessária para produzir determinada aceleração.
As forças num cabo de guerra
Ganha o jogo o grupo que conseguir deslocar o outro além do limite estabelecido



Força peso
A força mais comum no cotidiano é a força peso. É uma força de atração que atua em todos os corpos que estão sobre a superfície terrestre ou próximo a ela, que aponta para o centro da Terra.
Lembre-se de que, pela terceira lei de Newton, toda ação exercida por uma força provoca uma reação. Assim, a força peso também tem a sua reação, e ela se encontra sempre no centro da Terra e tem a mesma intensidade e a mesma direção, mas sentido oposto ao da força peso de um corpo.
Força peso: Uma pessoa “que pesa” 62 kg tem, na verdade, massa de 62 kg. Seu peso é a força gerada pela multiplicação dessa massa pela aceleração gravitacional (g = 9,8 m/s2).
O módulo da força peso pode ser expresso matematicamente por:
![]() → P é o módulo da força peso que atua sobre o corpo;
→ P é o módulo da força peso que atua sobre o corpo;
→ m é a massa do corpo;
→ g é o módulo da aceleração gravitacional exercida pela Terra sobre o corpo. Próxima à superfície terrestre, essa aceleração apresenta intensidade de aproximadamente 9,8 m/s2.
Desprezando-se a resistência oferecida pelo ar, quando uma maçã se desprende de uma árvore, está em queda livre, apenas sob a ação da força peso. Note que a força peso é exercida pela Terra sobre a maçã sem que haja nenhum contato físico entre os dois corpos.

Força normal
A força normal é a força que surge sempre que um objeto está em contato com uma superfície. É uma força perpendicular à superfície. Um corpo qualquer de peso ![]() pressiona a mesa,exercendo uma força sobre ela, e a superfície reage sobre o corpo, exercendo uma força de reação normal
pressiona a mesa,exercendo uma força sobre ela, e a superfície reage sobre o corpo, exercendo uma força de reação normal ![]() . Veja:
. Veja:
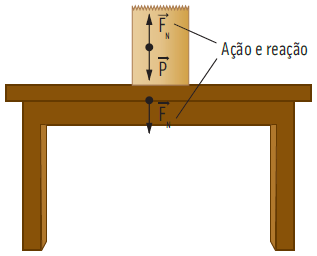

A força de ação e a força de reação nunca atuam no mesmo corpo. Assim, a força peso e a força normal nunca formam um par ação-reação. A reação da força peso está no centro da Terra.

Força de tração
A força de tração é a força que surge quando dois corpos quaisquer interagem por meio de um fio ou uma corda.
É a principal força atuante na brincadeira do cabo de guerra, num guindaste que eleva uma carga e no cabo de um guincho que reboca um automóvel. A função da corda ou do fio, no caso, é apenas transmitir a força entre os corpos.
Atrito
A força de atrito surge entre corpos que estão em contato. É uma força que se opõe ao movimento, ou à tendência de movimento, de um corpo em relação ao outro.
O módulo da força de atrito depende da intensidade de interação entre o objeto e a superfície sobre a qual ele se apoia. Depende, portanto, da força normal entre o objeto e a superfície. Quanto mais intensamente o objeto pressionar a superfície, maior será a força de atrito. Existem dois tipos de atrito:
Atrito dinâmico
Ou atrito cinético, ocorre quando os corpos estão em movimento um em relação ao outro. A expressão matemática para o módulo da força de atrito dinâmico é:
![]()
→ μc é o coeficiente de atrito cinético entre o objeto e a superfície. Lembrando: esse coeficiente é adimensional, ou seja, é um número puro, sem unidade;
→ N é a intensidade da força normal.
Atrito estático
Surge quando existe uma tendência de movimento, mas os corpos estão em repouso, um em relação ao outro. Matematicamente, o valor máximo da força de atrito estático é dado por
![]()
→ μe é o coeficiente de atrito estático entre o objeto e a superfície. Esse valor é um número puro, sem unidade;
→ N é a intensidade da força normal entre o objeto e sua superfície de apoio.
O atrito estático é sempre maior que o cinético. Por isso, é mais difícil começar a mover um objeto do que manter seu movimento.
Atrito versus força
O atrito estático é sempre maior que o cinético. O gráfico mostra os dois tipos de força de atrito ![]() em função da força
em função da força ![]() aplicada sobre um corpo
aplicada sobre um corpo
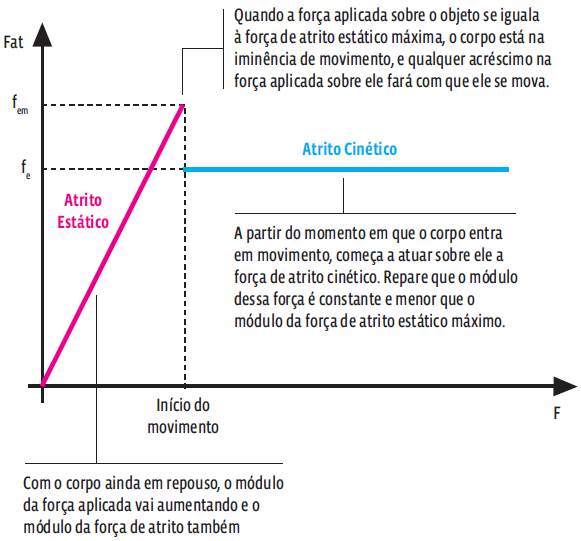
Agora vai!
Ao empurrar um guarda-roupa, o mais difícil é vencer o atrito estático.

Enquanto o guarda-roupa não estiver em movimento, a força de atrito estático sempre será igual à força aplicada sobre o móvel. Ou seja, a força de atrito estático é variável, vale o que tiver de valer para resistir ao movimento.

Quando a força exercida sobre o guarda-roupa supera o valor máximo da força do atrito estático, o móvel começa a se mover. A resistência ao movimento vem agora do atrito dinâmico, que tem valor constante e
ligeiramente menor que o valor do atrito estático.
Corpo em plano inclinado
É comum aparecerem nos exercícios de mecânica situações em que os corpos estão em superfícies inclinadas: um bloco de massa m apoiado sobre um plano inclinado formando um ângulo θ com a horizontal (veja abaixo). Para simplificar, desprezamos o atrito entre o bloco e o plano inclinado. Com isso, consideramos apenas duas forças atuando sobre o corpo: a força peso e a força normal:

Para encontrar a força resultante que atua sobre o corpo, devemos fazer a soma vetorial dessas forças. Note que as forças ![]() e
e ![]() q estão em direções distintas. A solução é decompor o vetor força peso em duas componentes ortogonais, uma delas na direção paralela à direção do plano inclinado (
q estão em direções distintas. A solução é decompor o vetor força peso em duas componentes ortogonais, uma delas na direção paralela à direção do plano inclinado ( ![]() ) e outra componente perpendicular ao plano inclinado (
) e outra componente perpendicular ao plano inclinado ( ![]() ):
):

A componente ![]() , perpendicular ao plano inclinado, equilibra-se com a força normal (
, perpendicular ao plano inclinado, equilibra-se com a força normal ( ![]() ). É esse equilíbrio que mantém o bloco em contato com a superfície. A componente
). É esse equilíbrio que mantém o bloco em contato com a superfície. A componente ![]() , paralela à direção do plano inclinado, é a própria força resultante na direção do movimento. É essa força resultante que causa a aceleração que faz o bloco escorregar. Por trigonometria podemos escrever as componentes da força peso como:
, paralela à direção do plano inclinado, é a própria força resultante na direção do movimento. É essa força resultante que causa a aceleração que faz o bloco escorregar. Por trigonometria podemos escrever as componentes da força peso como:
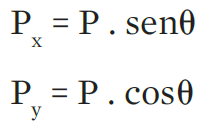
Qualquer força de atrito entre o bloco e o plano atuará sempre no sentido contrário ao sentido da tendência do movimento.

Círculo vicioso. Um catavento, sob uma corrente de ar contínua, mantém o módulo da velocidade escalar constante, num movimento circular uniforme
Movimento circular uniforme
O movimento circular uniforme (MCU) é aquele em que o objeto se desloca numa trajetória circular em torno de um ponto central, com módulo de velocidade escalar constante. É o movimento executado pelos ponteiros de um relógio, pelas rodas de um carro, por um carrossel ou uma roda-gigante no parque de diversão.
A alteração na direção de v indica que o movimento, embora uniforme, está sujeito à ação de uma aceleração. A aceleração que atua no MCU é chamada aceleração centrípeta e está sempre voltada para o centro da trajetória, alterando a direção e o sentido do vetor velocidade.

O módulo da aceleração centrípeta é:
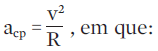
→ v é o módulo da velocidade escalar do corpo;
→ R é o raio da circunferência descrita pelo corpo.
Se existe uma aceleração sobre o corpo (a aceleração centrípeta), então existe uma força resultante que atua sobre ele na mesma direção e no mesmo sentido. Essa força, a força resultante centrípeta, que tem a mesma direção e o mesmo sentido da aceleração, está voltada para o centro da circunferência descrita pela trajetória.
O módulo da resultante centrípeta é dado pela mesma expressão da segunda lei de Newton:

Um corpo em MCU pode estar sob a ação de várias forças que atuam na direção radial. Combinadas, elas dão a força centrípeta resultante.

No MCU, o módulo de velocidade escalar do corpo é constante. Mas a direção do vetor velocidade se altera a cada instante, mantendo-se sempre tangente à trajetória.


Um carro em velocidade v constante passa sobre uma lombada, descrevendo um trecho circular de raio R. No ponto mais alto da trajetória, as forças que atuam na direção do centro da trajetória circular são as forças peso e normal. Veja:

Para que o carro execute a trajetória circular, deve haver uma força resultante apontando para o centro da circunferência. É a força resultante centrípeta, a soma vetorial de ![]() e
e ![]() . Então, FCP = P – N
. Então, FCP = P – N

Esta é a expressão que dá a força resultante centrípeta no movimento sobre a lombada.
Veja, também, que isolando a força normal N de um lado da igualdade, temos:
![]()
A massa do carro e a força P que atua sobre esse carro são constantes. Então, a intensidade da força normal, que mantém o carro sobre o solo, depende do raio da lombada e da velocidade com que o carro passa por ela. Quanto maior é a velocidade, menor é a força normal e mais o carro se descola da superfície. É o que dá aquela sensação de frio na barriga quando passamos muito rápido sobre uma lombada e descolamos um pouco do banco.










