Termologia: Transformações gasosas

A dinâmica dos gases

Gases são corpos muito especiais. São facilmente comprimidos ou expandidos. Além disso, as moléculas de corpos gasosos estão mais distantes e sempre mais agitadas do que nos sólidos e líquidos. Por isso, eles respondem de maneira diferente às alterações de temperatura.

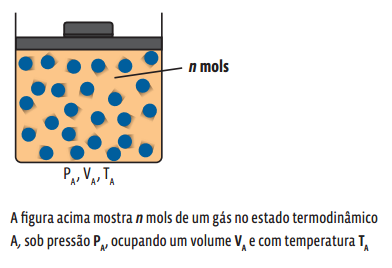
Um gás é caracterizado por três grandezas físicas: temperatura, volume e pressão. São as chamadas variáveis de estado, que definem o estado termodinâmico de um gás. Para facilitar o estudo dos gases, os físicos adotam um modelo científico que trata o gás como um gás ideal.

EQUAÇÃO DE CLAPEYRON

Num gás ideal, as três variáveis de estado (pressão, volume e temperatura) estão relacionadas com a quantidade de gás existente na amostra. A relação matemática se dá pela equação de Clapeyron, também chamada equação de estado dos gases ideais:

→ p é a pressão exercida pela amostra, medida em N/m2 ;

→ V é o volume ocupado pelo gás, medido em m3 ;

→ n é o número de mols da amostra (a quantidade de matéria);

→ R é a constante universal dos gases ideais (vale ≈ 8,31 J/mol.K);

→ T é a temperatura do gás, medida em Kelvin (K).

Mols: é a unidade do S.I. para a quantidade de matéria, medida em átomos, moléculas ou íons. Por definição, 1 mol contém 6,02 . 10²³ partículas. Esse valor é a constante de Avogadro. Em 1 mol de qualquer gás existem 6,02 . 10²³ moléculas.

Repare que todas as medidas acima foram dadas conforme estabelecidas no S.I. Mas a constante universal dos gases pode ser dada em outra unidade: R ≈ 0,082 atm . L /mol . K

A equação de Clapeyron relaciona as variáveis de estado de um gás que ocupa um único estado termodinâmico, ou seja, ela ainda não nos permite analisar o comportamento de uma amostra de gás que sofre alguma alteração em qualquer uma de suas variáveis de estado. Então, para determinado estado termodinâmico A, temos:

LEI GERAL DOS GASES IDEAIS

Uma transformação gasosa é caracterizada pela alteração do estado termodinâmico de um gás, ou seja, toda transformação gasosa está atrelada a uma alteração nas variáveis de estado que definem aquele gás. Podemos entender uma transformação gasosa como um procedimento que “leva” uma amostra gasosa de um estado termodinâmico inicial para um estado termodinâmico final. Uma amostra do gás A, aprisionada em um recipiente completamente vedado, em determinado estado termodinâmico inicial i, sofre uma transformação qualquer passando para um estado termodinâmico f.

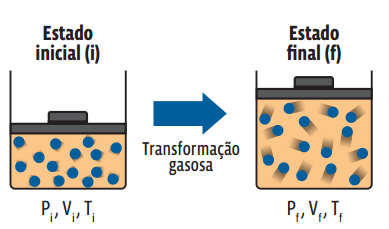
Repare que o recipiente é vedado. Então, não há alteração na quantidade de gás – ou seja, o número n de mols do gás se mantém constante durante a transformação. Como todas as três variáveis de estado se relacionam e não houve alteração na quantidade de gás, podemos igualar a equação de Clapeyron para cada um dos estados acima:

Para o estado inicial i:

Para o estado final f: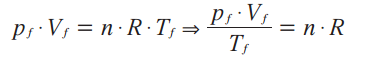

Repare que as duas equações acima são iguais a n . R. Então, elas são iguais entre si:

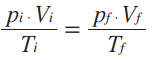
A equação indica que, numa amostra de gás ideal, em que não há variação de massa, essa relação entre temperatura, volume e pressão se mantém. Em uma transformação geral, qualquer alteração em uma das variáveis (digamos, a temperatura) afeta imediatamente as outras duas (volume e pressão) e o gás sofre transformação em seu estado termodinâmico. Quando alteramos apenas duas variáveis de estado e mantemos fixa a terceira, ocorrem as chamadas transformações particulares.

TRANSFORMAÇÃO ISOVOLUMÉTRICA

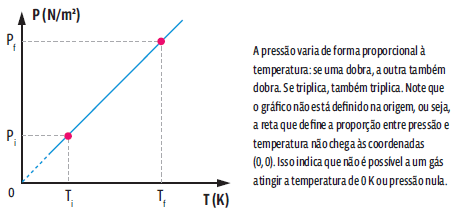
A transformação isovolumétrica (ou isocórica) ocorre sem que haja alteração no volume ocupado pela massa gasosa – ou seja, apenas a pressão e a temperatura sofrem mudança. Veja o que ocorre numa amostra de gás aprisionada em um recipiente rígido e indeformável que sofre alteração de temperatura:

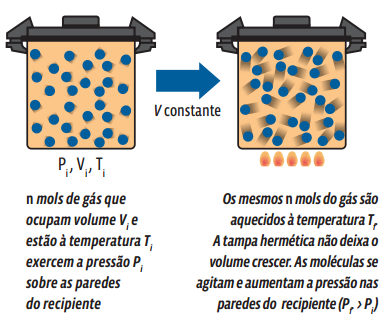
Matematicamente, a partir da lei geral dos gases ideais, concluímos que:

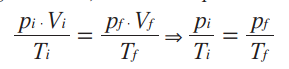
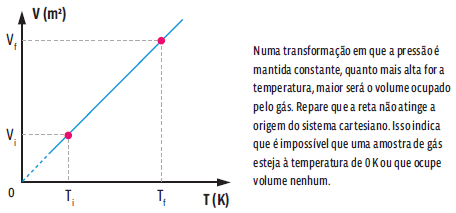
Essa relação matemática mostra que, numa transformação isovolumétrica, a pressão e a temperatura de um gás são grandezas diretamente proporcionais, ou seja, ao dobrarmos a temperatura da amostra de gás, verificamos que a pressão exercida por ele também dobra. Repare que as temperaturas são dadas em Kelvin. E, como não podemos fazer nenhuma divisão por zero, então é impossível que a amostra tenha, no início ou no final, temperatura de 0 K. Podemos representar essa transformação gasosa em um gráfico.

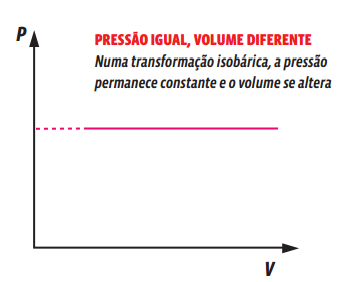
TRANSFORMAÇÃO ISOBÁRICA

Uma transformação gasosa que ocorre sem alteração de pressão é chamada isobárica. Veja o que acontece com uma amostra gasosa aprisionada num recipiente com um êmbolo móvel, ou seja, cujo volume pode ser alterado.

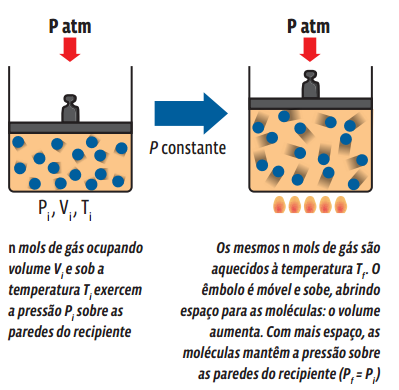
Matematicamente, a partir da lei geral dos gases ideais, temos:

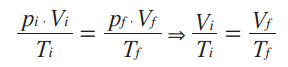
Essa relação matemática mostra que, numa transformação isobárica, o volume e a temperatura de um gás são grandezas diretamente proporcionais, ou seja, ao dobrarmos a temperatura da amostra de gás, o volume ocupado por ele também dobra. Podemos representar essa transformação gasosa em um gráfico que relacione as variáveis de estado desse gás.

As variações numa transformação isobárica podem também ser representadas pela relação entre pressão e volume:

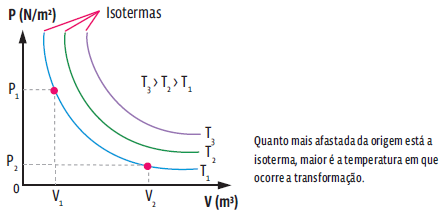
TRANSFORMAÇÃO ISOTÉRMICA

A transformação isotérmica é aquela na qual a temperatura da amostra de gás não se altera, ou seja, em uma transformação isotérmica, apenas as variáveis de estado pressão e volume sofrem alteração. Matematicamente, pela lei geral dos gases ideais, temos:

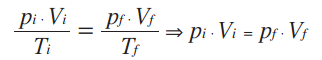
Note na expressão acima que, numa transformação em que a temperatura é constante, a pressão e o volume são grandezas inversamente proporcionais – ou seja, se uma sobe, a outra desce, porém, mantendo o produto entre elas constante. A representação de uma transformação isotérmica em um gráfico de pressão por volume se dá pela chamada curva isoterma.