Cinemática: Movimento Circular Uniforme

A FÍSICA DO GIRA-GIRA
O movimento de uma partícula que percorre uma trajetória circular com velocidade escalar (v) constante chama-se movimento circular uniforme (MCU). No cotidiano, o MCU é realizado, por exemplo, pelas pás de um ventilador, pelas rodas de um carro e pelos satélites artificiais que orbitam a Terra em velocidade constante.
No MCU, as condições e características do movimento se repetem em intervalos de tempo iguais. Portanto, esse tipo de movimento é considerado um fenômeno periódico. Por isso, no estudo do MCU adotamos as seguintes grandezas:


• Período (T): é o intervalo de tempo em que a partícula descreve uma volta completa (n = 1). A unidade para período, pelo SI, é o segundo (s).
• Frequência (f ): é a relação entre o número de voltas (n) dadas pela partícula e o tempo gasto para completar essas voltas (Δt).
Essa relação é expressa como:
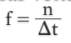
No dia a dia, usamos diversas unidades para a frequência, como rotações por minuto (rpm). Mas pelo SI a unidade para frequência é o hertz (Hz), que equivale a uma rotação por segundo.
GRANDEZAS ESCALARES E ANGULARES
As grandezas escalares usadas para o movimento de uma partícula em MCU são calculadas da mesma maneira como fazemos para movimentos retilíneos. Assim:

Mas no MCU, uma partícula muda constantemente de direção, em torno de um ponto central. Nesse caso, podemos analisar o movimento da partícula usando ângulos. Nesse caso, o deslocamento e a velocidade são grandezas angulares. A unidade básica para a medida de ângulos, no S.I., é o radiano (rad).
O deslocamento angular (∆φ) é o ângulo entre a posição da partícula em relação a um ponto de origem do movimento. Em linguagem matemática: ∆φ = φ – φ0. Repare que o deslocamento numa volta completa é de 360o, que equivalem a 2 π rad. O tempo gasto nesse deslocamento é igual ao período T. Portanto, o deslocamento no período é ∆φ = 2 π rad.
A velocidade angular (ω) é o deslocamento angular (∆φ) em dado intervalo de tempo (∆t).
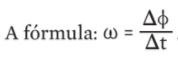
Uma das vantagens de trabalhar com a unida de radiano é que podemos estabelecer relações diretas entre grandezas escalares e grandezas angulares. Acompanhe o raciocínio:
Um corpo em MCU dá uma volta completa em um intervalo de tempo ∆t. Vamos calcular a velocidade escalar e a angular.
Para a velocidade escalar:

• o corpo dá uma volta completa. Isso significa que ele se desloca por toda a circunferência. Lembrando das aulas de geometria, temos C = 2 π R;
• e o tempo para dar essa volta completa é o período T.
• Portanto, podemos estabelecer a relação
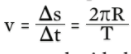
Para a velocidade angular (ω):
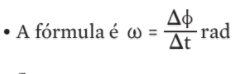
• Se o corpo percorreu uma volta completa, então ∆φ = 2 π e ∆t = T (período)
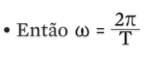
• Substituindo esses valores na fórmula da velocidade linear, temos
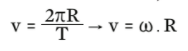
No MCU, o valor da velocidade é constante. Portanto, a aceleração escalar é nula. Mas, ao longo da trajetória circular, o corpo muda constantemente de direção. Isso significa que a velocidade vetorial se altera. Nesse caso, trabalhamos com a aceleração centrípeta (acp), sempre orientada para o centro da trajetória. Veja:
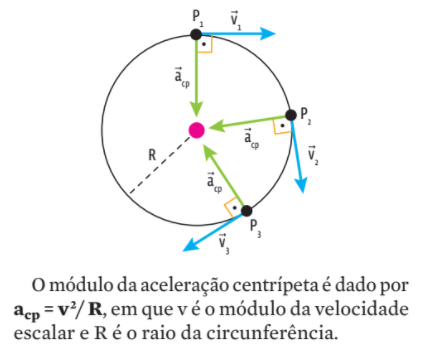
–

POLIAS E ENGRENAGENS
Uma aplicação das propriedades do MCU diz respeito ao estudo do acoplamento entre polias ou engrenagens. Veja a figura:
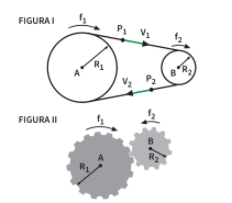
Repare:
• Na figura I, as polias A e B estão ligadas por uma correia. Isso é um acoplamento de polias. Repare que A e B giram no mesmo sentido. Já a fgura II, mostra o acoplamento de duas engrenagens. Note que elas giram em sentidos opostos.
• Em ambas, o módulo da velocidade escalar (v) de qualquer ponto da correia é a mesma, tanto para a engrenagem 1 quanto para a 2. (Lembre-se de que em termos vetoriais as velocidades estão sempre variando.)
• Em qualquer uma das figuras, as frequências e os períodos de cada par de polias são diferentes. Explicando: quanto maior o raio de uma polia, maior o tempo que ela levará para dar uma volta completa (ou seja, maior será seu período T). Portanto, menor será a sua frequência f. Neste caso, fB < fA. A relação entre a frequência de cada engrenagem é dada por:
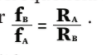
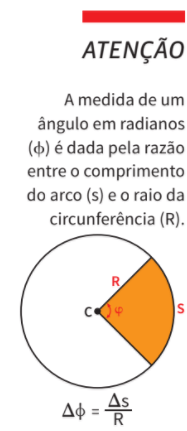
• Se as frequências são diferentes, o módulo das velocidades angulares também são diferentes. Da mesma maneira, temos aqui ωA < ωB. Se a velocidade escalar é a mesma, podemos estabelecer a relação entre as velocidades angulares: