Determinantes: Propriedades das matrizes quadradas
Algumas operações com matrizes que têm o mesmo número de linhas e de colunas facilitam cálculos, inclusive em geometria

Matrizes quadradas têm sempre associado a elas um número real, chamado determinante. Determinantes têm diversas aplicações em matemática – por exemplo, na definição da área de um triângulo (veja o quadro Na prática). Dependendo da ordem da matriz quadrada, existe uma regra específica para encontrar o determinante.
Determinante de matrizes 2 x 2
Considere a matriz
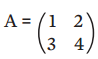
O determinante é calculado em três passos:
- primeiro, multiplicamos os valores da diagonal principal;
- segundo, multiplicamos os valores da diagonal secundária;
- e, terceiro, subtraímos o produto da diagonal secundária do produto da diagonal principal. Visualizando a explicação:
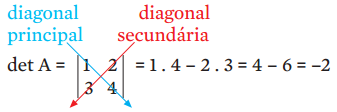
Portanto, o determinante da matriz A é –2.
Determinantes de matrizes 3 x 3
Para matrizes quadradas de ordem 3, o caminho para encontrar o determinante é um pouco diferente. Nesse caso, aplicamos a regra de Sarrus. Acompanhe o raciocínio, no exemplo abaixo, como se aplica essa regra, passo a passo.
Considere a matriz
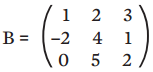
- Repetimos as duas primeiras colunas ao lado direito da matriz original.
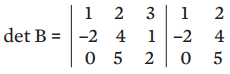
- Multiplicamos os valores da diagonal principal e das diagonais paralelas a ela:
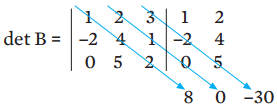
- Somamos os produtos dessa multiplicação: 8 + 0 – 30 = –22
- Fazemos o mesmo com a diagonal secundária:
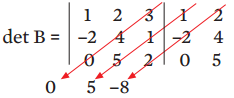
Somando os valores encontrados, temos: 0 + 5 – 8 = – 3
- Por fim, subtraímos os dois valores obtidos das duas diagonais:
![]()
Este é o determinante da matriz.
Propriedades dos determinantes
Conhecer algumas das propriedades dos determinantes facilita muito os cálculos.
1. Se todos os elementos de uma linha ou coluna de uma matriz A forem nulos, det A = 0. Ex:
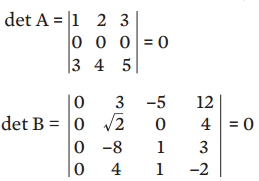
2. Se os elementos de duas linhas ou colunas de uma matriz A forem iguais ou proporcionais, então det A = 0. Ex:
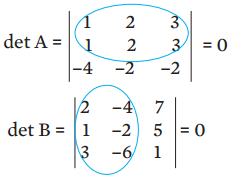
3. Se trocarmos a posição de duas linhas ou colunas, o valor do determinante tem o sinal invertido. Por exemplo:
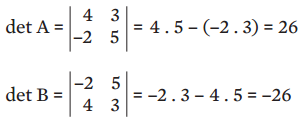

Por padrão, o determinante de uma matriz é indicado por um par de barras paralelas ao redor da matriz original.

ÁREA DE UM TRIÂNGULO
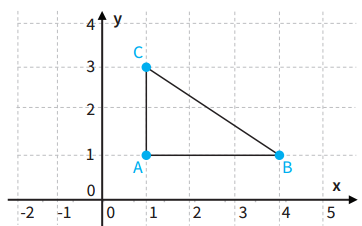
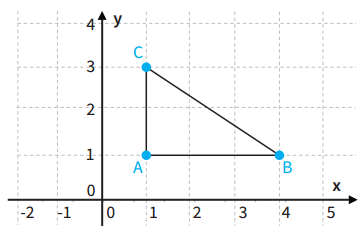
Qual a área do triângulo ABC da figura com vértices de coordenadas A (1, 1), B (4, 1) e C (1, 3)?

A área de um triângulo é dada pela fórmula
![]()
Portanto, para o triângulo medindo 2u e 3u, a área é
![]()
Agora veja a relação da área do triângulo com o determinante de uma matriz.
• Montamos a matriz referente aos pontos que definem o triângulo no plano cartesiano: A (1, 1), B (4, 1) e C (1, 3).
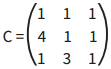
Repare que a primeira coluna traz os valores de x para A, B e C. A segunda coluna, os valores de y. A terceira coluna é completada apenas com 1.
• Calculando o determinante de C:
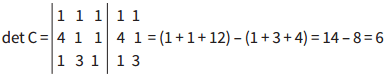
Veja:
- Repetimos as duas primeiras colunas ao lado da matriz original. Fazendo a multiplicação das duas diagonais e subtraindo um valor pelo outro, temos:
![]()
- O determinante da matriz C é exatamente o dobro da área do triângulo.
Detalhe: A área de uma figura é sempre um valor positivo. Por isso, o valor do determinante deve ser apresentado como módulo (valor absoluto)

Quando o determinante se referir à área de um triângulo, o resultado será sempre dado em módulo do valor – ou seja, em valor absoluto. Isso porque área é uma grandeza física que nunca pode ter valor negativo.

Matrizes
MATRIZES São como tabelas, nas quais cada elemento ocupa uma posição determinada: linha i e coluna j. O número de linhas (m) e de colunas (n) define a ordem da matriz. Por exemplo, A23 é uma matriz com 2 linhas e 3 colunas. Matrizes quadradas são aquelas que têm o mesmo número de linhas e de colunas. Qualquer matriz tem duas diagonais:

MATRIZ IDENTIDADE É aquela na qual a diagonal principal contém apenas o valor 1, e os demais elementos são iguas a 0:
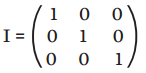
OPERAÇÕES COM MATRIZES Na soma ou subtração de duas matrizes, fazemos a operação entre elementos correspondentes. Por exemplo na soma de A22 + B22, fazemos: a11 + b11, a12 + b12, a21 + b21 etc. Na multiplicação de uma matriz por um número, multiplicamos o número, separadamente, pelos elementos. Por exemplo, se uma matriz for multiplicada por 2, fazemos a11 . 2, a12 . 2, a21 . 2, a22 . 2 etc. A multiplicação entre duas matrizes só é possível quando o número de linhas de uma matriz é igual ao número de colunas de outra. Os elementos da matriz P produto de A1 . A2 são obtidos pela multiplicação dos elementos de cada linha de A1 pelos elementos correspondentes de cada coluna de A2. Depois, os resultados são somados.
DETERMINANTE É um número real (k) que pode ser associado a determinada matriz quadrada. O determinante de matriz 2 x 2 é encontrado pela soma da multiplicação dos valores da diagonal principal com o produto dos valores da diagonal secundária. Para matrizes 3 x 3, seguimos a regra de Sarrus: copiamos as duas primeiras colunas à direita da matriz original; multiplicamos os valores da diagonal principal e, também, das diagonais paralelas; somamos esses produtos. Fazemos o mesmo com os valores da diagonal secundária e suas paralelas. Por fim, subtraímos os valores.
PROPRIEDADE DOS DETERMINANTES Se todos os elementos de uma linha ou uma coluna de uma matriz A forem iguais a zero, então o determinante da matriz é zero (det A = 0) . Se duas linhas ou duas colunas tiverem elementos iguais ou proporcionais, o determinante da matriz é igual a zero também. Se trocarmos de posição duas linhas ou duas colunas