Termologia: Dilatação

CRESCE E ENCOLHE – Construída com ferro, a torre Eiffel, em paris, pode variar sua altura em até 18 centímetros nos dias mais quentes de verão. Ela também se expande na direção horizontal no decorrer do dia, por causa do sol que bate numa ou noutra face
O tamanho varia em função do calor
Construir uma ponte, uma torre ou um viaduto que resista ao vai vém de veículos não depende apenas do emprego de material de boa qualidade. Os engenheiros precisam calcular, também, o efeito que as forças naturais exercem sobre a obra. Entre esses efeitos, um dos mais importantes é a dilatação térmica. Com raras exceções, todo material aquecido se expande. E essa expansão resulta no aumento do comprimento e da largura de uma ponte, ou na altura de um edifício. Se o material usado não tiver espaço para se dilatar, a estrutura poderá ficar comprometida.
Os engenheiros costumam, então, intercalar o material básico da construção com as juntas de dilatação – frestas vazias ou preenchidas por outro material, que se dilata menos com o aumento da temperatura.
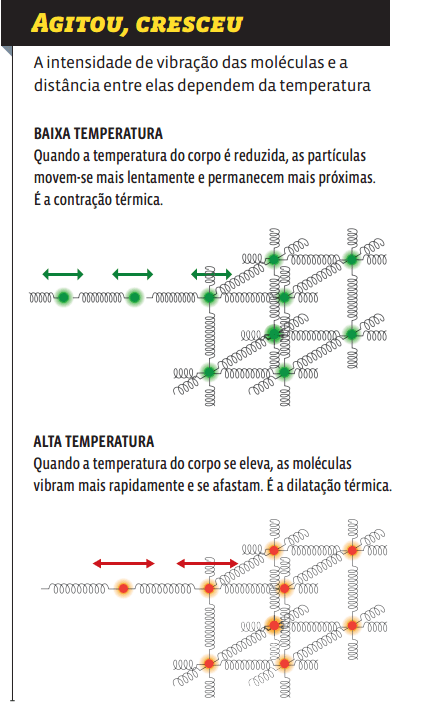
Quando a temperatura de um material se eleva, o grau de agitação de suas moléculas cresce e elas se afastam. Se as partículas que constituem um corpo estão mais afastadas, então esse corpo ocupa um espaço maior. Isso é o que chamamos dilatação térmica. No sentido inverso, quando um corpo é resfriado, a agitação de suas partículas diminui. Essa redução na agitação das moléculas faz com que o corpo diminua suas dimensões. É a contração térmica.
Qualquer corpo sólido que tenha a temperatura alterada apresenta variações em todas as suas dimensões. Mas podemos simplificar o fenômeno estudando apenas as dilatações ou contrações mais significativas – seu comprimento, sua área ou seu volume. Em qualquer um desses casos, a variação das dimensões do objeto depende de três parâmetros:
→ o tamanho inicial do corpo (comprimento, área ou volume inicial);
→ a alteração da temperatura a que o corpo foi submetido (Δθ);
→ o tipo de material que constitui o corpo.
DILATAÇÃO LINEAR
É a variação no tamanho de um corpo sólido cuja única dimensão significativa é o comprimento.Essa é a variação mais importante, por exemplo, nos trilhos de trem ou cabos de alta tensão.
O parâmetro que define a capacidade que determinado material tem de se dilatar ou se contrair ao longo de seu comprimento é o chamado coeficiente de dilatação linear (a).
Podemos, então, escrever a relação matemática que define a variação do comprimento de um corpo em função da variação de temperatura:
![]()
→ ∆L é a variação do comprimento do corpo;
→ L0 é o comprimento inicial do corpo;
→ a é o coeficiente de dilatação linear do material;
→ ∆θ é a variação de temperatura do corpo.
A unidade de medida mais usual do coeficiente de dilatação linear é °C-1 .
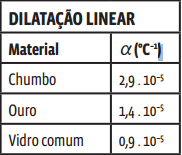
Nos sólidos, o coeficiente de dilatação é muito baixo. Isso demonstra que os efeitos de dilatação e contração são relativamente pequenos quando sua temperatura varia poucos graus Celsius. Por exemplo: a cada grau que se aquece uma barra de chumbo de 1 metro, ela aumenta seu comprimento em apenas 0,000029 m – ou seja, 0,029 mm. Veja o índice de dilatação linear de alguns materiais na tabela abaixo:

VÃO DE ESCAPE – As juntas de dilatação permitem que o piso se acomode quando é aquecido e não se quebre

LICENÇA PARA ESTICAR – Um vão de poucos centímetros a cada 20 metros impede que o trilho se expanda e se deforme com o calor
 DILATAÇÃO SUPERFICIAL
DILATAÇÃO SUPERFICIAL
Quando submetemos um corpo sólido de espessura desprezível a uma variação de temperatura, ocorre uma dilatação ou contração superficial – o corpo sofre variação significativa em sua área. É o que ocorre, por exemplo, com chapas de metal, de cimento ou de vidro.
O coeficiente de dilatação superficial é representado por , e sua unidade mais usual é, também, o °C-1. A relação matemática que define a variação superficial de um corpo qualquer é:
![]()
→ ∆A é a variação da área sofrida pelo corpo;
→ A0 é a área inicial do corpo;
→ β é o coeficiente de dilatação superficial do material que constitui o corpo;
→ ∆θ é a variação da temperatura do corpo.
A relação entre coeficiente de dilatação superficial (β) de um material e seu coeficiente de dilatação linear (α) é dada por:
![]()
Assim, o chumbo, cujo coeficiente de dilatação linear é 2,9 . 10-5 °C-1, tem um coeficiente de dilatação superficial igual a:
![]()
DILATAÇÃO VOLUMÉTRICA DOS SÓLIDOS
Quando um corpo sólido que tem todas as dimensões significativas é submetido a uma variação de temperatura, ocorre uma dilatação ou contração volumétrica – seu volume varia. Nos sólidos, essa dilatação é importante, por exemplo, em peças de encaixe, como parafusos e roscas, e de equipamentos ou aparelhos que serão submetidos a grande variação de temperatura.
Neste caso, em que consideramos a dilatação em três dimensões, trabalhamos com o coeficiente de dilatação volumétrico, representado por γ.
A relação matemática que define a variação do volume de um corpo em função da variação de temperatura é:
![]()
→ ∆V é a variação de volume sofrida pelo corpo;
→ V0 é o volume inicial do corpo;
→ γ é o coeficiente de dilatação volumétrica do material que constitui o corpo;
→ ∆θ é a variação da temperatura do corpo. A unidade mais usual para o coeficiente de dilatação volumétrica é, também, °C-1 .
O coeficiente de dilatação volumétrica pode ser relacionado com o coeficiente de dilatação linear de um mesmo material. A expressão matemática que expressa essa relação é:
![]()
Então, novamente no exemplo do chumbo, o coeficiente de dilatação volumétrica é fornecido por:
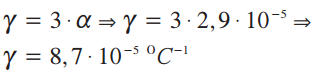
![]()
Corpos ocos se dilatam como se não fossem ocos. Um aro de metal (que tem um orifício no centro) se dilata como se fosse um disco compacto. Essa relação vale tanto para dimensões lineares (raio e diâmetro do centro oco), quanto para a superfície (área do centro) ou, no caso de uma esfera oca, para volume.

FACHADA MÓVEL – As lâminas de vidro da fachada de um edifício são encaixadas com certa folga para que não se quebrem quando sofrem dilatação superficial, em dias mais quentes
![]()
O coeficiente de dilatação linear de um material que constitui uma barra de 100 cm de comprimento inicial e que expandiu 0,016 cm quando submetido a uma variação de temperatura de 10 °C é assim calculado:
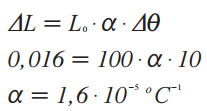
Ou seja, esse material tem seu comprimento alterado em 0,000016 centímetro para cada centímetro de comprimento inicial da barra quando submetido a uma variação de temperatura de 1 °C, ou ainda em 0,000016 metro para cada metro de comprimento inicial da barra quando submetido a uma variação de temperatura de 1 °C.
DILATAÇÃO DE LÍQUIDOS
Assim como no caso dos sólidos, quando aquecemos ou resfriamos um líquido também alteramos o grau de agitação de suas moléculas. Mas, nos líquidos, a força de coesão que mantém agrupadas essas partículas é bem menor que nos sólidos. Além disso, eles assumem o formato do recipiente que os contém. Assim, sempre que se fala em dilatação – ou contração – de um líquido, trata-se, no geral, de dilatação ou contração de seu volume.
A variação de volume (∆Vliq) de um líquido qualquer depende da variação de temperatura (∆θ) a que foi submetido, depende de seu volume inicial (V0 ) e também depende do líquido que estamos aquecendo ou resfriando. A relação matemática que define a variação do volume de um líquido em função da variação de temperatura é a mesma que define a variação de volume num sólido:
![]()
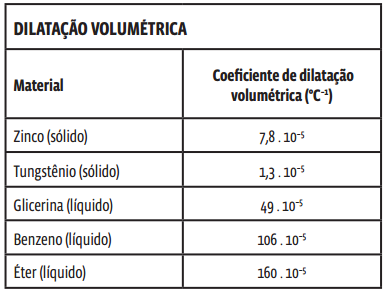
Justamente por envolverem uma força menor de coesão entre as moléculas, os líquidos apresentam maiores variações de volume do que os sólidos quando submetidos à mesma variação de temperatura.
Esse fato pode ser comprovado quando analisamos a tabela que compara os valores de coeficientes de dilatação volumétricos de sólidos e líquidos. Repare que os coeficientes de dilatação volumétricos dos líquidos são significativamente maiores que os dos sólidos.
 DILATAÇÃO APARENTE E REAL
DILATAÇÃO APARENTE E REAL
É preciso ter cuidado ao estudar a dilatação ou contração dos líquidos. Quando certa massa de líquido contida num recipiente é aquecida, seu volume varia. Mas não se pode esquecer que o aquecimento faz variar, também, o volume do recipiente (vidro ou qualquer tipo de metal) que o contém. Assim, podemos falar em dois tipos de dilatação do líquido: dilatação aparente e dilatação real.
A dilatação dos líquidos é significativamente maior que a dilatação dos sólidos. Então, quando um recipiente de vidro ou de metal, cheio de líquido, é aquecido, a tendência é que uma porção do líquido transborde. O volume de líquido que extravasa do recipiente se refere à dilatação aparente do líquido. Para calcular a dilatação real do líquido, temos de levar em consideração também a dilatação do recipiente. Matematicamente:
![]()
As equações que definem a variação de volume continuam valendo: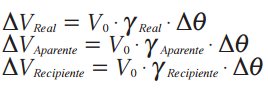
Como todo o conjunto é submetido à mesma variação de temperatura, podemos relacionar os coeficientes de dilatação volumétrico da seguinte maneira:![]()
Repare que o coeficiente de dilatação real do líquido depende apenas da natureza do líquido. Já o coeficiente de dilatação aparente do líquido varia de situação a situação, pois depende, também, do material de que é feito o recipiente no qual o líquido está contido.