Matrizes: Prateleiras matemáticas

Matrizes são como tabelas, em que as células são organizadas em linhas e colunas

Partindo direto de um exemplo você entende facilmente o conceito de matriz. As duas tabelas abaixo foram montadas pelo proprietário de uma loja para controle do estoque. A loja comercializa camisetas com quatro estampas diferentes, em três tamanhos e em modelagem masculina e feminina.

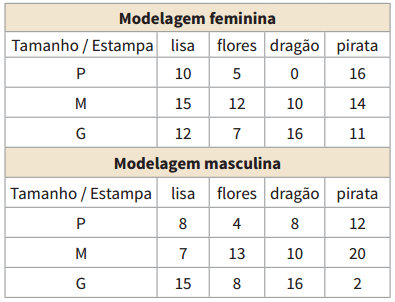
Cada uma dessas tabelas corresponde a uma matriz:

Para as camisetas femininas, a matriz A₁ :

Para as camisetas masculinas, a matriz A₂:

Analisando as duas matrizes:

• As matrizes trazem apenas células com valores numéricos. Não há cabeçalho ou título, como numa tabela. Isso porque quem criou a matriz sabe exatamente o que significa cada linha e cada coluna. E as linhas e colunas trazem valores ordenados e posicionados segundo a lógica do criador da tabela;
• Uma matriz pode ser escrita dentro de parênteses ou de colchetes, não faz diferença;
• A₁ e A₂ têm três linhas e quatro colunas. Então, são matrizes de ordem 3 x 4. Na notação de uma matriz genérica, o número total de linhas é chamando m; o número de colunas, n;
• Numa matriz de ordem 3 x 4, o número total de elementos é 12;
• Cada valor da matriz ocupa uma casa única, no cruzamento de determinada linha com determinada coluna. Então, qualquer valor está no cruzamento m x n;
• Para uma matriz genérica A, dizemos então que o elemento a_ij está no cruzamento da linha i com a coluna j. Por exemplo, na matriz A₁ , do nosso exemplo, o elemento de valor 5 ocupa a primeira linha e a segunda coluna. Dizemos então que, em A₁ , a₁₂ = 5 (lê-se “a um-dois é igual a 5”).

A notação A = (a_ij)_{m x n} indica que a matriz A é formada pelos elementos a_ij. Se A tem m linhas e n colunas, então 1 ≤ i ≤ m e 1 ≤ j ≤ n, sendo que m e n ∈ N.

Ou seja, qualquer elemento a da matriz tem de estar numa posição i x j que seja menor ou igual ao número total de linhas (m) e colunas (n).

Soma de matrizes

Só é possível somar ou subtrair matrizes com o mesmo número de linhas e colunas. Seguindo com o exemplo da loja de camisetas:

O estoque de camisetas por estampa e tamanho é dado pela soma das matrizes S = A₁ + A₂:

A matriz S traz a soma de camisetas conforme o tamanho e a estampa. Por exemplo, existem 20 camisetas com estampa de dragão, no tamanho M (a₂₃).

Repare que a célula ocupada por um valor é definida da mesma forma como definimos um ponto no plano cartesiano, por um par ordenado.

Multiplicação de matriz por um número k

Seguindo com nosso exemplo: quantas camisetas de cada tipo existiriam em estoque se o comerciante triplicasse a quantidade de cada uma delas? Basta multiplicar por 3 cada elemento da matriz S. Veja:

Diferentemente do que ocorre com a multiplicação de números reais, com matrizes, em muitos casos, a ordem dos fatores pode alterar o produto.

Multiplicação de matrizes

• A multiplicação só é possível se o número de colunas de uma matriz for igual ao número de linhas da outra matriz;
• Assim, a matriz produto P da multiplicação de A₁ por A₂ tem o número de colunas de uma das matrizes e o número de linhas da outra;
• Os elementos de P são obtidos pela multiplicação dos elementos de cada linha de A₁ pelos elementos correspondentes de cada coluna de A₂ . Depois, os resultados são somados.

Ainda no exemplo das camisetas: O comerciante quer saber o valor do estoque, em reais. O custo de cada peça varia segundo a estampa – o tamanho não importa, segundo a tabela:

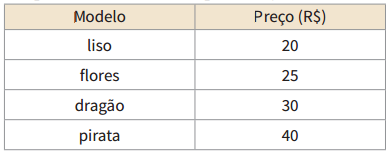
A matriz correspondente a essa tabela é:

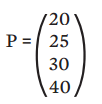
A matriz S, soma de A₁ e A₂:

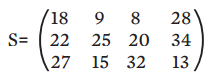
Repare: cada linha de S traz camisetas de um mesmo tamanho, mas com estampas diferentes. Se o valor em reais varia conforme a estampa, então cada valor das linhas de S deve ser multiplicado pelo valor correspondente de P.

Repare:

• A matriz P traz o valor, em reais, do estoque, conforme o tamanho das camisetas.
• O número de colunas da primeira matriz é igual ao número de linhas da segunda;
• S . P tem o número de linhas da primeira matriz e o número de colunas da segunda.

Matriz identidade

É uma matriz quadrada – ou seja, com número de linhas (i) igual ao número de colunas (j) – cujos elementos são 1 ou zero.

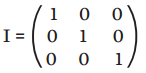
Repare que o valor 1 aparece apenas numa diagonal entre as posições em que i = j (a₁₁, a₂₂, a₃₃ etc.). Esta é a diagonal principal. Para as demais posições, o valor é zero.

A multiplicação de uma matriz por sua matriz identidade é sempre igual à matriz original.