Como estudar Matemática para o Enem
Veja quais são os temas mais recorrentes e como se preparar

O GUIA DO ESTUDANTE conversou com professores de cada matéria para descobrir quais são os temas mais cobrados no Enem. Eles analisaram as provas aplicadas desde 2009 (ano em que o exame passou a ter o formato atual) e apontaram não só quais os temas mais pedidos, mas também de que forma costumam ser cobrados. Veja a seguir os pontos mais importantes de Matemática:
Os temas mais recorrentes de Matemática
| Alguns dos assuntos mais recorrentes no Enem desde 2009 |
| Funções |
| Cálculo de área, volume e perímetros |
| Seno, cosseno e tangente |
| Probabilidade |
| Análise combinatória |
| Progressão aritmética e geométrica |
A prova de Matemática costuma ser uma das mais temidas pelos alunos, especialmente no Enem, que cobra 45 questões da disciplina. No entanto, de acordo com o professor Eduardo Izidoro, do Cursinho Henfil, a prova apresenta questões com vários níveis de dificuldade, e as perguntas realmente complicadas são mais raras.
A prova é forrada de gráficos, tabelas, esquemas e infogramas que devem ser interpretados com cuidado, mas, segundo o professor, “muito se engana quem acredita que se trata somente de uma prova de interpretação”. Para ele, a análise dos dados apresentados é constante na prova, mas não é suficiente sem as aplicações de conhecimentos específicos.
Na plataforma do Curso Enem GE, você encontra videoaulas, textos e exercícios sobre esse e todos os outros temas importantes para o Enem e outros vestibulares. Conheça clicando aqui.
No entanto, de acordo com Glenn Albert Jacques van Amson, professor do Curso Anglo, os conhecimentos específicos que a prova cobra são menos “cabeludos” do que se imagina. “Podemos dizer que 99% das perguntas englobam conteúdo do nono ano do Ensino Fundamental e primeiro ano do Ensino Médio”, afirma o professor. “Logaritmo já caiu na prova e exigiu que o candidato soubesse de cor suas propriedades, mas foi uma exceção”, diz.
O professor Marcus Aquino, do cursinho Oficina do Estudante, indicou os temas com maior probabilidade de serem cobrados na prova. Confira:
Funções de 1° e 2° graus
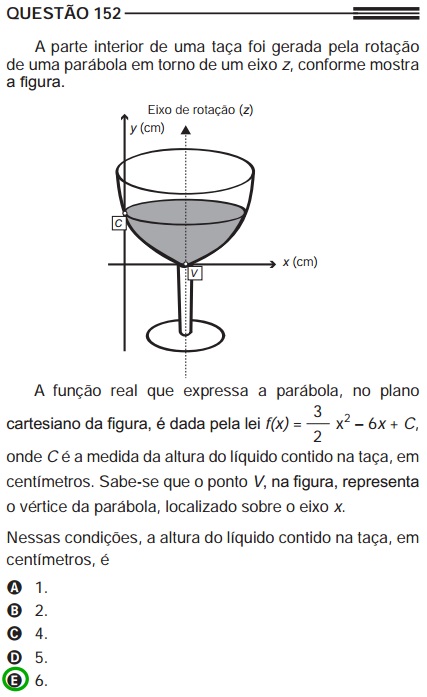
As questões de função podem aparecer com as mais variadas abordagens. No exemplo, a expressão f(x) (que indica a função) já aparece de cara na questão, sem exigir que o aluno faça maior esforço para decifrar qual operação será usada. No entanto, esse tipo de questão não é recorrente. Normalmente, o enunciado propõe uma situação em que o uso da função será necessário, mas sem deixar claro no texto.
Exemplo: questão retirada do Enem 2013 (resolução)
Progressão aritmética e geométrica
Com a progressão aritmética (PA) e a geométrica (PG), acontece uma situação parecida com a das funções. “Em um vestibular tradicional, uma questão de PA é anunciada com a frase “Em uma PA…”. No Enem isso também pode ocorrer, mas existe a preferência em se criar uma situação que origine uma PA. O aluno deve reconhecer que se trata de uma PA analisando os dados apresentados”, explica o professor Eduardo Izidoro.
Exemplo: questão retirada do Enem 2013 (resolução)

Estatística
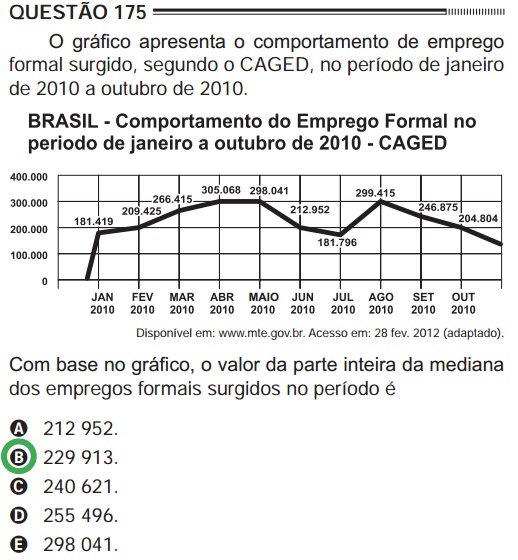
Nas questões de estatística, é bastante comum que caia a média aritmética, a moda ou a mediana.
Exemplo: questão retirada do Enem 2012 (resolução)
Grandezas proporcionais
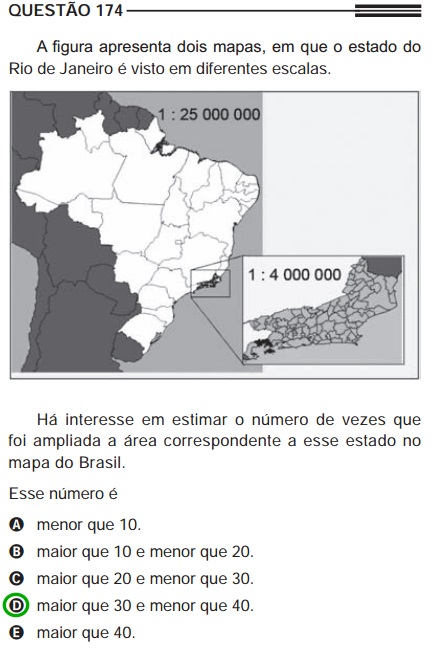
As questões que envolvem grandezas podem ser cobradas como inversamente proporcionais ou diretamente proporcionais. É bastante comum que sejam resolvidas com uma simples regra de três.
Exemplo: questão retirada do Enem 2013 (resolução)
Porcentagem
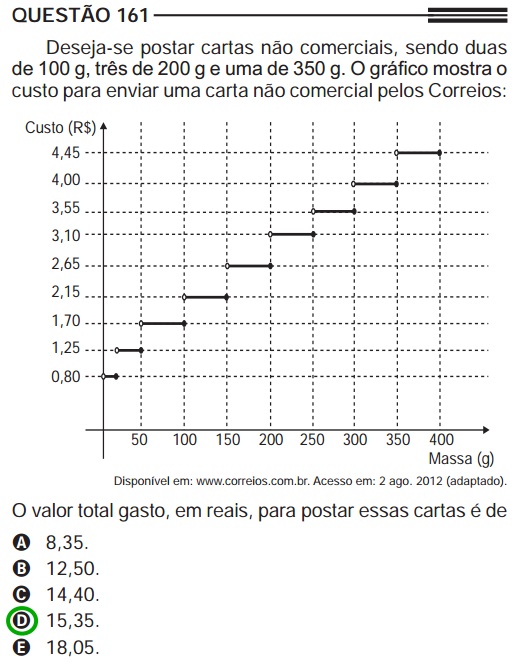
As questões de porcentagem também costumam apresentar um enunciado claro. No entanto, muitas vezes a questão que traga porcentagem também aborda outro assunto – o mais comum é que seja matemática financeira, por exemplo.
Exemplo: questão retirada do Enem 2013 (resolução)

Equações 1º e 2º graus
As questões que exigem uma equação são bastante comuns e também não costumam ter um enunciado explícito. Normalmente, a questão coloca um problema que exige que o aluno formule uma relação de equação para resolver.
Exemplo: questão retirada do Enem 2013 (resolução)
Trigonometria (triângulo retângulo e semelhança de triângulos)
Já nas questões de trigonometria, o uso das relações matemáticas costuma ser bem mais aparente. Normalmente, a questão já vem com um desenho da figura, deixando claro o que o aluno deve fazer para chegar à resposta.
Exemplo: questão retirada do Enem 2013 (resolução)
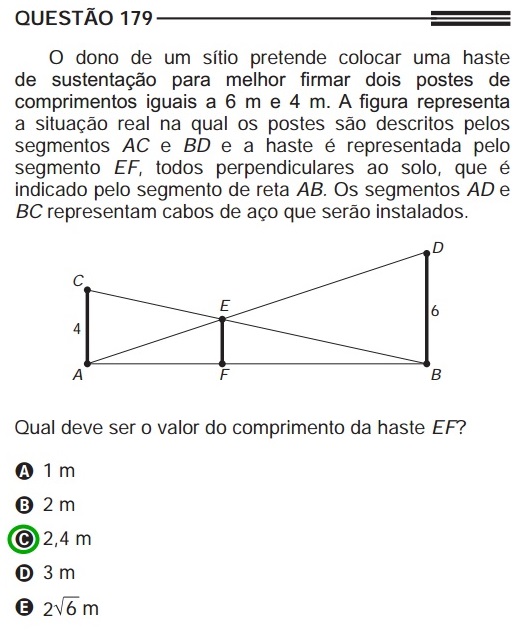
Áreas de figuras planas/prismas, cilindros, cones e esferas
Da mesma forma que nas questões de trigonometria, as questões de figuras planas e figuras tridimensionais (área e volume) costumam apresentar a figura do objeto descrito no texto.
Exemplo: questão retirada do Enem 2013 (resolução)
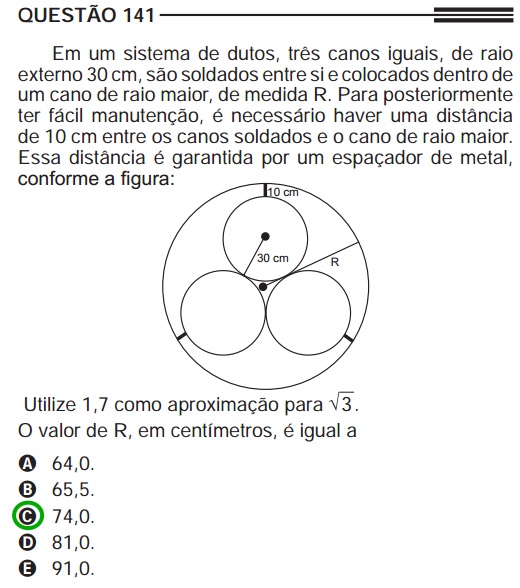
Análise combinatória e probabilidade
Exemplo: questão retirada do Enem 2013 (resolução)
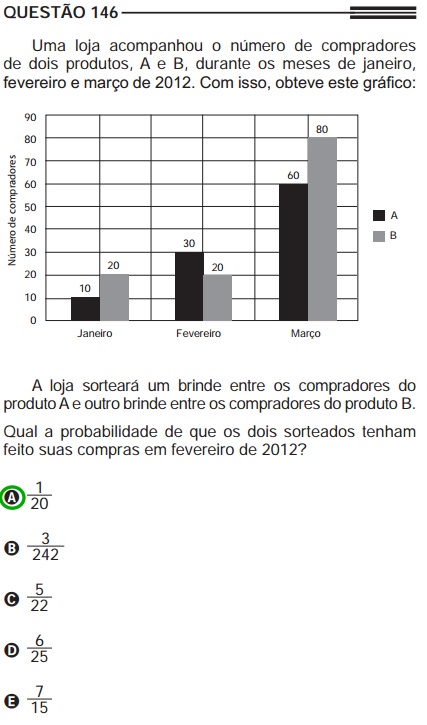
Exemplo: questão retirada do Enem 2013 (resolução)
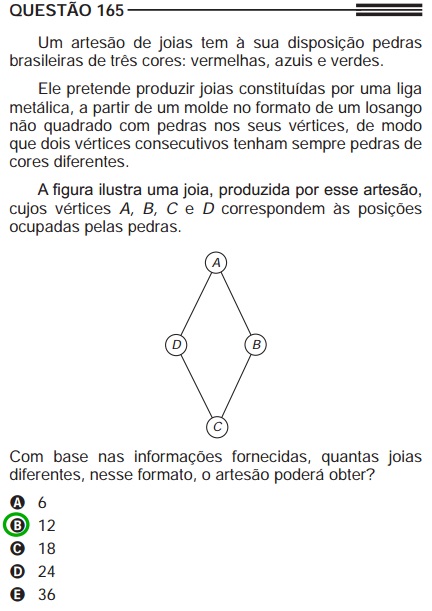
Como se sair bem
A maior dica do professor Glenn (e que vale para as outras matérias também) é resolver questões antigas de provas anteriores. Aproveite as que estamos postando por aqui e clique nos links para ter acesso a todas as questões. “Fazendo isso, o aluno vai se sentir bem mais à vontade na hora do exame”, completa.
Outra coisa que ajuda é usar o método pega-varetas. No jogo, que consiste em lançar varetas ao chão e pegar o máximo possível sem movimentar as outras, o segredo é sempre pegar as que estavam mais fáceis para, só depois, tentar tirar as difíceis.
Esse princípio também se aplica ao Enem e ao vestibular, em que há um grande número de questões de diferentes níveis de dificuldade e um tempo limitado para resolvê-las. Assim, comece respondendo as mais fáceis e deixe as mais complicadas para depois. “As questões têm pesos diferentes, mas o candidato deve tentar responder o maior número que conseguir”, explica o professor. Se perder muito tempo nas mais difíceis, sobrará pouco para as que você teria mais chance de acertar, certo?


 Como se escreve: Bob Good, Bobbie Goods ou Bob Gude?
Como se escreve: Bob Good, Bobbie Goods ou Bob Gude? Qual o masculino de capivara?
Qual o masculino de capivara? “Tons pastéis” ou “tons pastel”: qual é o certo?
“Tons pastéis” ou “tons pastel”: qual é o certo? Baixe o PDF do edital do CNU 2025 aqui
Baixe o PDF do edital do CNU 2025 aqui Eles já tinham diploma e emprego, mas decidiram migrar de carreira com a Inteligência Artificial
Eles já tinham diploma e emprego, mas decidiram migrar de carreira com a Inteligência Artificial








