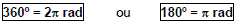Ângulos – Geometria Básica

São regiões formadas por duas semi-retas com um ponto O em comum chamado origem. Os dois princi-pais sistemas de medidas são:

Circular
Sua unidade principal é o radiano (rad); tem como base o ângulo central de uma circunferência cujo arco tem a mesma medida do raio.

Sexagesimal
Sua unidade principal é o grau ( º ); tem como base a divisão da circunferência em 360 partes iguais, sendo cada uma dessas partes um grau.
Possui os submúltiplos minuto( ’ ) e segundo ( ” ), cujas equivalências são: 1º = 60’ e 1’ = 60″.

Relação entre os sistemas

Tipos de Ângulos

a) Ângulo Agudo: 0º < A < 90º 

b) Ângulo Reto: A = 90º 

c) Ângulo Obtuso: 90º < A < 180º 

d) Ângulo Raso ou Meia Volta: A = 180º 

e) Ângulos Opostos pelo Vértice (OPV): São congru-entes os ângulos AOC e BOD. 

f) Ângulos Consecutivos: Possuem um lado e um vértice em comum. 
Exemplos: ângulos AOB e AOC; AOB e BOC. 

g) Ângulos Adjacentes: São ângulos consecutivos que não possuem pontos internos em comum.
Exemplo: ângulos AOB e BOC. 

h) Ângulos Complementares: Ângulos que somados resultam em 90º.
OBS: Complemento de um ângulo é o valor que falta para a soma completar 90º. 

i) Ângulos Suplementares: Ângulos que somados seu valor resulta em 180º.
OBS: Suplemento de um ângulo é o valor que falta para a soma completar 180º. 

j) Ângulos Replementares: Ângulos que somados resultam em 360º.
OBS: Replemento de um ângulo é o valor que falta para a soma completar 360º.

(UFMG) Na figura, OM é a bissetriz do ângulo AOB, ON é a bissetriz do ângulo BOC e OP é a bissetriz do ângulo COD. A soma POD + MON é igual a:

Retas paralelas cortadas por uma transversal

Macete! Regra do Z: Os ângulos formados pela letra “Z” (direita ou invertida) são sempre congruentes.

(FUVEST) Na figura, as retas r e s são paralelas, o ângulo 1 mede 45º e ângulo 3 mede 55º. A medida, em graus, do ângulo 2 é:

a) 50º
b) 55º
c) 60º
d) 80º
e) 100º

Solução: Traçando uma reta auxiliar paralela às outras duas, teremos que o ângulo do meio é igual a soma dos ângulos extremos; com isso temos que:

x = 45º + 55º
x = 100º
Letra e)

Macete! 
Regra do M: O ângulo do meio da letra “M” é igual a soma dos ângulos extremos.

Ângulo formado pelos ponteiros do relógio 

Macete! Quando é solicitado o ângulo formado entre os ponteiros da hora e dos minutos, podemos resolver a questão usando a seguinte formula:

(UFRRJ) Considere um relógio cujos ponteiros movi-mentam-se proporcionalmente.
Calcule o valor em graus do menor ângulo formado pelos ponteiros quando esse relógio marcar 14:45h.

Solução: Pela fórmula temos:

Dica! Quando o valor da hora é acima de 12h, podemos considerar seu valor congruente; no exemplo anterior se considerarmos 2h 45min, teremos:

Como o ângulo pedido é o menor, temos que calcular o replemento: 360 – 187,5 = 172,5º ou 172º 30´