Círculo Trigonométrico – Trigonometria
Compartilhe essa matéria: Link copiado! É aquele no qual seu centro também é centro de eixos coordenados e cujo raio é unitário (R = 1). Relações Fundamentais Do triângulo OBM, temos sen α = MB/OB, mas como OB = R = 1, temos que Siga ENTRAR NO CANAL GOOGLE NEWS Seguir no Instagram Seguir […]
Por
SEGUIR
SEGUINDO
26 fev 2012, 17h45 • Atualizado em 16 Maio 2017, 13h48
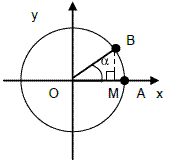
É aquele no qual seu centro também é centro de eixos coordenados e cujo raio é unitário (R = 1).
Relações Fundamentais
Do triângulo OBM, temos sen α = MB/OB, mas como OB = R = 1, temos que 
Cos α = OM/OB, mas OB = R = 1; logo 
Como OBM é retângulo, vale o Teorema de Pítágoras. Logo temos OB2 = OM² + MB², ou seja:
Definimos secante de um ângulo (sec α) como o inverso do cosseno, ou seja:
sec α = 
Definimos cossecante de um ângulo (cossec α ) como o inverso do seno, ou seja:
cossec α = 
Definimos cotangente de um ângulo (cotg α) como o inverso da tangente, ou seja:
cotg α = 
Relações decorrentes
Dividindo a formula (I) por cos2α , temos: 
Dividindo a fórmula (I) por sen2α , temos: 
Quadrantes
Cada um dos semiplanos situados no círculo trigono-métrico são chamados quadrantes.
Os pontos A, A’, B e B’ são chamados pontos quadran-tais (entre um quadrante e outro).
Os sinais do seno e cosseno variam conforme os quadrantes da seguinte forma:
Intervalo de Variação
Por causa do raio unitário do círculo trigonométrico, tanto os valores de sen α quanto cos α são limitados entre -1 e 1, ou seja:
Redução de Quadrantes
São deduzidas fórmulas para calcular sen x, cos x, tg x e derivados, relacionando o ângulo x com algum elemento do 1º quadrante.
(UFF) Seja x um arco do primeiro quadrante tal que sen x = 0,6. Pode-se afirmar que:
Solução: Da relação sen2x + cos2x = 1 teremos que cos x = 0,8.
Letra d)
Como somar a nota do Enem e calcular a média
A TRI do Enem 2025 falhou? Especialista no método de correção explica
8 ótimos livros que dá para ler em um único final de semana
UFPR 2026: veja lista de aprovados no vestibular
Confira estratégias de como usar a nota do Enem 2025 no Sisu
