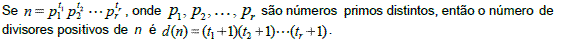Divisibilidade – Aritmética Básica
Compartilhe essa matéria: Link copiado! Número Primo Possui exatamente dois divisores naturais distintos: ele mesmo e a unidade. Observe que: – O número 1 não é primo; – São primos menores que 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, […]
Por
SEGUIR
SEGUINDO
18 fev 2012, 16h15 • Atualizado em 16 Maio 2017, 13h50
Número Primo
Possui exatamente dois divisores naturais distintos: ele mesmo e a unidade. Observe que:
– O número 1 não é primo;
– São primos menores que 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
– Números primos entre si são 2 (ou mais) números inteiros que têm como divisor comum apenas a unidade Exemplo: 5 e 9 são primos entre si, mesmo 9 não sendo primo.
– Para saber se um número é primo, basta dividi-lo pela sucessão dos números primos até que o quoci-ente seja menor ou igual ao divisor.
Número Composto
Todo número natural não primo maior que 1(número composto) que pode ser decomposto como produto de fatores primos.
Cálculo do Número de Divisores Positivos 
Exemplo:
Calcule os divisores positivos de 60. Fatorando, temos que 60 = 2² x 3¹ x 5¹
Logo, o número de divisores positivos de 60 é: d(60) = (2 + 1) . (1 + 1) . (1 + 1) = 3 . 2 . 2 = 12
Cuidado! Se a questão pedir quantidade de divisores inteiros (positivos e negativos!); então você deve dobrar o valor dado pela fórmula d(n).
Na questão anterior, por exemplo, o número de diviso-res inteiros seria 160.2 = 320.
Algumas Regras de Divisibilidade
Por 2: o algarismo das unidades é par.
Por 3: a soma dos algarismos é um múltiplo de 3.
Por 4: o número termina em 2 zeros ou os 2 últimos algarismos à direita do número formam múltiplo de 4.
Por 5: o algarismo das unidades é 0 ou 5.
Por 6: divisível por 2 e por 3 simultaneamente.
Por 8: o número termina em 3 zeros ou os 3 últimos algarismos da direita formam um múltiplo de 8.
Por 9: a soma dos algarismos é um múltiplo de 9.
(UNIFESP – 08) O 2007° dígito na seqüência:
12345432123454321234543… é:
a) 1
b) 2
c) 3
d) 4
e) 5
Solução: Observe que a seqüência é formada por 12345432 (8 números) repetidas vezes!
Logo como o 2007º terá de ser um desses 8 números, para saber qual deles é, basta dividir 2007 por 8; teremos 2007 → 8 = 250.8 + 7; logo é o 7º número da seqüência.
Letra c)
Dica! Seqüências nunca são aleatórias, portanto não “chute”, pois é uma questão fácil; observe que sempre existe padrão de repetição, que pode ser numa se-qüência repetitiva de números, letras, símbolos, etc…
