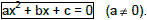Toda equação com a forma  .
.
Suas raízes são obtidas pela fórmula de Báskara

onde  é chamado discriminante da equa-ção, pois detalha uma das três situações a seguir:
é chamado discriminante da equa-ção, pois detalha uma das três situações a seguir:

Equação a partir da Soma e Produto das Raízez
Também podemos achar as raízes através dos valores da soma e do produto delas. Quando a = 1, toda equação do 2º grau assume a seguinte estrutura:

onde a soma (S) e o produto (P) são calculados pelas fórmulas abaixo:
Soma das Raízes (S): 
Produto das Raízes (P): 
Dica: Qualquer expressão com as raízes da equação do 2º grau podem (e devem) ser expressas pela soma e/ou produto das raízes (basta uma “manipulação algébrica” na expressão).
Exemplo:
Sejam r e s as raízes da equação:

O valor numérico da expressão (r + s + 1)(r + s – 1) é:
a) 2/7
b) 3/7
c) 9/7
d) 4/3
e) 2

(FUVEST) A soma e o produto das raízes da equação do 2º grau (4m + 3n)x² – 5nx + (m – 2) = 0 valem, respectivamente, 5/8 e 3/32.
Então m + n é igual a:
a) 9
b) 8
c) 7
d) 6
e) 5

Sistemas do 2º grau
Quando o sistema possui a forma

e onde resolvendo esse tipo de sistema, acabaremos caindo em uma equação do 2º grau.
Exemplo
A área de um retângulo é igual a 32 cm². Se a altura mede 4 cm a menos que a base, qual a medida da base do retângulo?
Solução: Chamando a base e a altura por B e h, res-pectivamente, teremos: B. h = 32 e H = B – 4
B.(B – 4) = 32 portanto B² – 4B – 32 = 0 → B = 8 e h = 4cm
Dica: Muito comum problemas do 2º grau envolvendo partilha de dívida entre pessoas; sempre podemos considerar implicitamente tratarem-se de divisões exatas.
(UNESP) Um grupo de x estudantes se juntou para comprar um computador portátil (notebook) que custa R$ 3.250,00. Alguns dias depois, mais três pes-soas se juntaram ao grupo, formando um novo grupo com x + 3 pessoas. Ao fazer a divisão do valor do computador pelo número de pessoas que estão com-pondo o novo grupo, verificou-se que cada pessoa pagaria R$ 75,00 a menos do que o inicialmente pro-gramado para cada um no primeiro grupo. O número x de pessoas que formavam o primeiro grupo é:
a) 9
b) 10
c) 11
d) 12
e) 13
Solução: Chamando x o número de estudantes e y a quantia a ser paga por cada um, teremos:
x.y = 3250 (I) e (x + 3).(y – 75) = 3250 (II)
(II) xy – 75x + 3y + 225 = 3250 portanto 75x – 3y = 225 (÷ 3)
25x – y = 75 → y = 25x – 75 Substituindo em (I), temos:
(I) x(25x – 75) = 3250 portanto 25x² – 75x – 3250 = 0 (÷ 25)
x² – 3x – 130 = 0 de onde tiramos x = – 10 (não serve) e x = 13 estudantes.
Letra e)




 Qual é o plural de lápis?
Qual é o plural de lápis? Gabarito oficial do Enem 2024: confira todos aqui
Gabarito oficial do Enem 2024: confira todos aqui Questão de Física do Enem 2024 é anulada; veja qual
Questão de Física do Enem 2024 é anulada; veja qual Confira nota de corte da Unicamp 2025 primeira fase
Confira nota de corte da Unicamp 2025 primeira fase 5 dicas de última hora para quem não leu os livros obrigatórios da Fuvest
5 dicas de última hora para quem não leu os livros obrigatórios da Fuvest