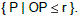Esferas – Geometria Espacial
É o lugar geométrico de todos os pontos P do espaço cuja distância a um ponto fixo O é menor ou igual a um número positivo r, ou seja: A superfície esférica é Seção de uma Esfera A interseção de um plano com uma esfera é um círculo. Esse círculo é máximo quando passa pelo […]
É o lugar geométrico de todos os pontos P do espaço cuja distância a um ponto fixo O é menor ou igual a um número positivo r, ou seja: 
A superfície esférica é 
Seção de uma Esfera
A interseção de um plano com uma esfera é um círculo. Esse círculo é máximo quando passa pelo centro da esfera.

Se d é a distância do centro O ao plano, r é o raio da interseção e R, o raio da esfera, então: 
Volume e Área da Esfera
Se o volume da esfera é V e a área da superfície esfé-rica é S, então:

Cunha Esférica e Fuso Esférico 
(UNIFESP) Um inseto vai se deslocar sobre uma superfície esférica de raio 50 cm, desde um ponto A até um ponto B, diametralmente opostos, conforme a figura.

O menor trajeto possível que o inseto pode percorrer tem comprimento igual a:


(UFRJ) Considere um retângulo, de altura y e base x, com x > y , e dois semicírculos com centros nos lados do retângulo, como na figura abaixo.

Calcule o volume do sólido obtido pela rotação da região sombreada em torno de um eixo que passa pelos centros dos semicírculos.
Solução: O volume do sólido será dado pela diferença entre os volumes do cilindro e das duas metades da esfera que juntas somam uma esfera inteira, ou seja:


 SEGUIR
SEGUIR
 SEGUINDO
SEGUINDO

 Como se escreve: Bob Good, Bobbie Goods ou Bob Gude?
Como se escreve: Bob Good, Bobbie Goods ou Bob Gude? Qual o masculino de capivara?
Qual o masculino de capivara? “Tons pastéis” ou “tons pastel”: qual é o certo?
“Tons pastéis” ou “tons pastel”: qual é o certo? Baixe o PDF do edital do CNU 2025 aqui
Baixe o PDF do edital do CNU 2025 aqui Eles já tinham diploma e emprego, mas decidiram migrar de carreira com a Inteligência Artificial
Eles já tinham diploma e emprego, mas decidiram migrar de carreira com a Inteligência Artificial