Geometria Espacial – Conceitos Iniciais

Postulados

São afirmações aceitas sem demonstração. Relacionam as noções primitivas de ponto, reta e plano.

Postulado de Existência
Numa reta e num plano existem infinitos pontos (dentro e fora dele).

Postulados de Determinação
Dois pontos distintos determinam uma única reta que passa por eles;
Três pontos não colineares determinam um único plano que passa por eles.

Postulado da Inclusão
Se uma reta tem 2 pontos distintos num plano, então ela está contida no plano.

Postulado das Paralelas
Por um ponto passa uma única reta paralela a uma reta dada.

Este último é conhecido como postulado de Euclides (300 a.C.). É a propriedade que caracteriza a Geometria Euclidiana.

Determinação de Planos
Um plano pode ser determinado de quatro modos:

– por 3 pontos não colineares;
– por uma reta e um ponto fora dela;
– por 2 retas concorrentes;
– por 2 retas paralelas distintas.

Posições relativas entre retas
Podem ser concorrentes, paralelas ou reversas.

a) Concorrentes: duas retas distintas são concorrentes se, e somente se, tiver um único ponto comum.

b) Paralelas: duas retas distintas são paralelas se, e somente se, forem coplanares e não tiverem ponto comum.

c) Reversas: duas retas distintas são reversas se, e somente se não existe plano que as contenha.

Posições relativas entre reta e plano
Pode a reta estar contida, ser secante ou ser paralela com o plano.

a) Contida: Se, e somente se garantirmos que pelo menos dois pontos da reta estejam no plano.

b) Concorrentes ou secantes: Se, e somente se, têm um único ponto comum.

c) Paralelas: Se, e somente se, não tiverem ponto comum.

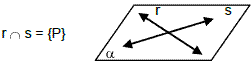
Posições relativas entre planos
Podem ser paralelos ou secantes entre si.

a) Paralelos: Se, e somente se, não tem ponto co-mum.

b) Secantes: Se, e somente se, se interceptarem, sen-do essa intersecção uma reta.

(UNIFESP) Dois segmentos dizem-se reversos quando não são coplanares. Neste caso, o número de pares de arestas reversas num tetraedro, como o da figura, é:

a) 6
b) 3
c) 2
d) 1
e) 0

Solução: Ao tomarmos as arestas de base (BC, CD e BD), vemos que as retas AD, AB e AC são suas res-pectivas retas reversas, e com isso temos ao todo TRÊS pares de retas reversas.
Letra b) 

(UNIFESP) Considere o sólido geométrico exibido na figura, constituído de um paralelepípedo encimado por uma pirâmide.
Seja r a reta suporte de uma das arestas do sólido, conforme mostrado.

Quantos pares de retas reversas é possível formar com as retas suportes das arestas do sólido, sendo r uma das arestas do par?

a) 12
b) 10
c) 8
d) 7
e) 6

Solução:

Teremos QUATRO arestas da pirâmide de vértice do topo em comum, mais QUATRO assinaladas de faces do paralelepípedo não adjacentes, num total de OITO arestas.
Letra c)