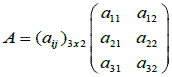Matrizes – Álgebra Linear
Compartilhe essa matéria: Link copiado! Matriz Retangular do tipo m x n (lê-se “m por n”) é uma tabela de valores dispostos em m linhas (horizontais) e n colunas (verticais). Denotamos por aij ao elemento da linha i e da coluna j. Se A é uma matriz do tipo m x n, escrevemos: Matriz Quadrada […]
Por
SEGUIR
SEGUINDO
25 fev 2012, 14h22 • Atualizado em 16 Maio 2017, 13h49
Matriz Retangular do tipo m x n (lê-se “m por n”) é uma tabela de valores dispostos em m linhas (horizontais) e n colunas (verticais).
Denotamos por aij ao elemento da linha i e da coluna j.
Se A é uma matriz do tipo m x n, escrevemos:
Matriz Quadrada
Chamamos matriz quadrada de ordem n uma matriz em que o número de linhas é igual ao de colunas. Exemplos:
Matriz Linha
Possui uma única linha, ou seja, é da forma 1 x n.
Exemplos:
Matriz Coluna
Possui uma única coluna, ou seja, é da forma n x 1.
Exemplos:
Matriz Nula (O)
É uma matriz quadrada onde todos os seus elementos são iguais a zero.
Exemplos:
Matriz Identidade (I)
É uma matriz diagonal onde os elementos da diagonal principal são iguais a unidade, ou seja:
Matriz Simétrica
É a matriz que se iguala a sua transposta, ou seja:
Exemplos:
Matriz Anti-simétrica
É a matriz oposta da simétrica, ou seja: 
Exemplos:
Operações entre Matrizes
Soma e Subtração de Matrizes
Só podemos realizá-las entre matrizes do mesmo tipo.
Multiplicação de Matrizes
A multiplicação entre matrizes possui a seguinte regra: o número de colunas da 1ª matriz deverá ser igual ao número de linhas da 2ª matriz, ou seja:
Propriedades da Adição de Matrizes
A + B = B + A (comutatividade)
A = (B + C) = (A + B) + C (associatividade)
A + O = O + A = A (elemento neutro é a matriz nula)
A + (- A) = O (-A é a matriz oposta)
Propriedades da Multiplicação de Matrizes
(AB)C = A(BC) = ABC (associatividade)
(A + B)C = AB +AC (distributiva à direita)
A(B + C) = AB + AC (distributiva à esquerda)
k(AB) = (kA)B = A(kB) (k é um escalar)
A.I = I.A = A (elemento neutro é a matriz identidade)
A . O = O. A = O
a) -112
b) -18
c) – 9
d) não existe
e) nda
Cuidado! De maneira geral A.B diferente de B.A (uma armadilha fatal para muitos vestibulandos!!! )
(UFRJ) Considere as matrizes
Seja A² = A . A e B² = B. B
Determine a matriz C = A² – B² – (A + B) (A – B).
Solução: Observe que C = A² – B² – A² + AB – BA + B² = AB – BA, pois A.B diferente de B.A.
Então teremos que:
Qual o coletivo de uva?
Luzinhas ou luzezinhas de Natal: qual é o plural?
O significado da palavra “frangalhos” – que não tem nada a ver com frango!
Por que dizer “assistir o filme” está errado, mesmo sendo tão comum no português
Se o seu sonho é ser médico, a Medicina Santo Amaro pode ser o caminho
