Pirâmides – Geometria Espacial
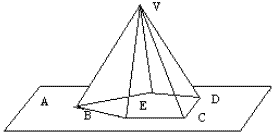
Compartilhe essa matéria: Link copiado! Priorizar nos meus resultados Google Chamamos de pirâmide ao poliedro que possui todos os vértices em um plano, chamado plano de base, exceto um, denominado vértice da pirâmide. Pirâmide Regular Quando a base é um polígono regular e a projeção ortogonal do vértice sobre o plano da base é […]
Por
SEGUIR
SEGUINDO
26 fev 2012, 16h05 | Atualizado em 16 Maio 2017, 13h49
Chamamos de pirâmide ao poliedro que possui todos os vértices em um plano, chamado plano de base, exceto um, denominado vértice da pirâmide.
Pirâmide Regular
Quando a base é um polígono regular e a projeção ortogonal do vértice sobre o plano da base é o centro desta. Em uma pirâmide regular as arestas laterais são iguais e consequentemente as faces laterais são triângulos isósceles iguais.
Elementos da Pirâmide
AB – aresta da base
VA – aresta lateral
VO – altura
VM – apótema
OM – apótema da base
O A – raio da circunferência circunscrita (R)
As relações entre os elementos de uma pirâmide regular através dos triângulos retângulos conforme indicados na figura, são:
Superfície e Volume
Área Lateral: SL = soma das áreas de todas as faces laterais.
Área Total: 
Volume: 
Seções Transversais e Tronco de Pirâmide
Considere uma pirâmide qualquer de altura h, seccio-nada por um plano paralelo a base e distante d do vértice. O polígono da seção é semelhante à base, sendo a razão de semelhança igual a K = d/h.
Valem as seguintes relações:
O volume do tronco de pirâmide de bases paralelas é igual a diferença dos volumes das pirâmides (V – v), ou seja:
(UFF) A grande pirâmide de Quéops, antiga construção localizada no Egito, é uma pirâmide regular de base quadrada, com 137m de altura. Cada face dessa pirâmide é um triângulo isósceles cuja altura relativa à base mede 179m.
A área da base dessa pirâmide, em m2, é:
a) 13272
b) 26544
c) 39816
d) 53088
e) 79432
Solução: Seja L/2 metade do lado do quadrado da base; por Pitágoras temos:
(L/2)2 + 1372 = 1792
L2/4 = 1792 -1372 = (179 + 137).(179 – 137) = 13.273
L2 = 4 x 13.273 = 53088
Letra d)
(FUVEST) Um telhado tem a forma da superfície lateral de uma pirâmide regular, de base quadrada. O lado da base mede 8 m e a altura da pirâmide 3 m. As telhas para cobrir esse telhado são vendidas em lotes que cobrem 1 m2. Supondo que possa haver 10 lotes de telhas desperdiçadas (quebras e emendas), o número mínimo de lotes de telhas a ser comprado é:
a) 90
b) 100
c) 110
d) 120
e) 130
Solução: Sendo base quadrada, teremos 4 triângulos para calcular a área; precisamos primeiro achar a altura h do triângulo de face. Então por Pitágoras faremos:
h2 = (L/2)2 + H2 = 42 + 32 portanto h = 5
Área Lateral = 4.8.5/2 = 80 m2, que dariam 80 lotes + 10 lotes (perdas) dão total de 90 lotes.
Letra a)
