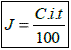Porcentagem – Aritmética Básica

Compartilhe essa matéria:

Link copiado!

São frações cujo denominador é o número 100.

Exemplos:

40/100 = 0,40 corresponde a 40%
135/100 = 1,35 corresponde a 135%
6897/100 = 68,97 corresponde a 6897%
0,28/100 = 0,0028 corresponde a 0,28%

Siga

ENTRAR NO CANAL

GOOGLE NEWS

Seguir no Instagram

Seguir no YouTube

Seguir no Facebook

Seguir no X

Seguir no Tiktok

Fatores de Aumento e Redução

Uma mercadoria deverá ter seu preço aumentado em 20%. Basta multiplicarmos seu preço antigo por 1,20 pois 100% + 20% é igual a 120% = 1,20.
Neste caso 1,20 é denominado fator de aumento.

Se o preço de uma mercadoria deve ser diminuído em 20%, o fator multiplicador é 0,80, pois 100% menos 20% é igual a 80%. Logo 0,80 é chamado fator de desconto (ou redução).

Cuidado!
Fatores de aumento sempre são maiores que 1.
Fatores de redução sempre estão entre 0 e 1.

Dica:
Podemos usar mais de um fator e também misturá-los (aumento e redução) numa mesma ques-tão.

Exemplo: 
Dois aumentos sucessivos de 10% numa mercadoria correspondem a um aumento único de quantos por cento?

Solução:
Não são “óbvios” 20%, pois o 2º aumento é em cima da mercadoria já aumentada em 10%.
Supondo a mercadoria com preço P, teremos:
P.(1,10).(1,10) = P.(1,21), ou seja, um aumento de 21% (100% + 21% = 121% = 1,21).

Exemplo: 
Sobre o valor de uma certa compra foram feitos dois abatimentos sucessivos de 10% e 15%. Calcule o desconto único que substituiria os dois aba-timentos:

Solução: 
Basta aplicar os dois fatores de desconto na mercadoria de preço P.
Logo: P.(0,90).(0,85) = P.(0,765) e assim teremos um desconto de 23,5% (100% – 76,5% = 23,5%).

(FUVEST) Na reprodução de uma figura, a primeira cópia obtida reduziu em 30% a área desta figura. A seguir, esta cópia foi reproduzida com ampliação de 40%. A área da figura obtida na segunda cópia, comparada com a área da figura original, é:

a) 98% menor 
b) 90% maior 
c) exatamente igual 
d) 90% maior 
e) 2% menor

Solução: 
Chamando a área inicial de X, teremos:
X. (0,70).(1,40) = X.(0,98) ou seja, 2% menor letra e)

Juros Simples
Juro é a remuneração de um capital aplicado (ou uma compensação pelo pagamento de uma dívida), a partir de um prazo determinado.
Podemos calcular os juros simples através da formula:

onde C é o capital, i é a taxa e t o tempo.

Montante
É a soma do capital (C) mais os juros (J). 

Cuidado!
Antes de usar a fórmula, a taxa de juros (ao dia, ao mês ou ao ano) e tempo (dias, meses, anos) devem estar na mesma unidade. 

Não esquecer que problemas de juros geralmente consideram mês e ano comercial, ou seja:
mês comercial tem 30 dias e ano comercial 360 dias.

Exemplo: A quantia de 4 milhões foi aplicada durante 5 dias a uma taxa mensal de 36%. Qual o montante após a aplicação? 

Solução: O valor dos juros simples é dado por:
J = 4.000.000 x 5/30 x 36/100 = 240.000
Logo, o montante será: M = 4.000.000 + 240.000
M = R$ 4.240.000,00

(UFMG) Um capital de R$ 30.000,00 foi dividido em duas aplicações: a primeira pagou uma taxa de 8% de juros anuais; a outra aplicação, de risco, pagou uma taxa de 12% de juros anuais. Ao término de um ano, observou-se que os lucros obtidos em ambas as apli-cações foram iguais. Assim sendo, a diferença dos capitais aplicados foi de:

a) R$ 8.000,00 
b) R$ 4.000,00
c) R$ 6.000,00 
d) R$ 10.000,00

Solução: Fazendo X + Y = 30.000, teremos:

de onde tiramos 2X = 3Y e resolvendo o sistema temos X = 18.000 e Y = 12.000. 

Finalmente, a diferença de capitais será dada por: X – Y = 18.000 – 12.000 = 6.000 Letra c)

• Mais lidas

1

Atualidades

De quem é a Groenlândia? Entenda onde fica a ilha e por que Trump quer tomá-la

2

Estudo

O único plural da língua portuguesa em que o “s” vai no meio da palavra

3

Universidades

Como consultar as vagas do Sisu 2026?

4

Estudo

Qual é o feminino de urubu?

5

Universidades

Saiba qual é o curso com mais vagas no Sisu 2026