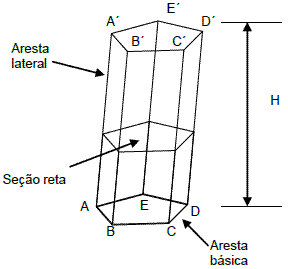
Prisma de Revolução
É o sólido formado por uma superfície prismática fechada e por dois planos paralelos que interceptam todas as geratrizes.
Os polígonos congruentes determinados sobre esses planos pela superfície são as bases do prisma; os outros, suas faces laterais.
Altura de um prisma é a distancia H entre suas bases.

Um prisma é dito triangular, quadrangular, pentago-nal, etc … conforme suas bases sejam triângulos, quadriláteros, pentágonos, etc …
Um prisma é reto ou obliquo conforme suas arestas laterais sejam perpendiculares ou oblíquas às bases.
Seção reta é a seção obtida no prisma por um plano perpendicular as arestas laterais.
Prisma regular é o prisma reto cujas bases são polí-gonos regulares.
Áreas do Prisma
Área lateral (SL) é a soma das áreas das faces late-rais.
Área total (ST) é a soma da área lateral com as áreas das bases.

Volume do Prisma
É por definição o produto da área de sua base pela altura, ou seja:

Paralelepípedo retângulo
É todo prisma reto cujas bases são retângulos.
Obtemos a área, o volume e o comprimento da diago-nal desse paralelepípedo, de dimensões a, b e c.

Da figura acima calculamos os seguintes valores:
Área do paralelepípedo retângulo:

Volume do paralelepípedo retângulo:

Diagonal do paralelepípedo retângulo: 
Cubo
É o paralelepípedo retângulo cujas faces todas são quadrados.
Área total do Cubo
É igual a seis áreas de um quadrado de lado a, ou seja:

Volume do Cubo 
Diagonal do Cubo
Como as arestas são iguais, isto é a = b = c, então a diagonal é dada por: 
Dica! Procure olhar as figuras espaciais nas três vistas (frontal, lateral e superior), e use principalmente as duas últimas que não são convencionais; você acaba resolvendo questões mais facilmente.
(FUVEST) O cubo de vértices ABCDEFGH, indi-cado na figura, tem arestas de comprimento a. Sabendo-se que M é o ponto médio da aresta AE, então a distância do ponto M ao centro do quadrado ABCD é igual a:

Solução: No triângulo retângulo da figura abaixo, aplicando Pitágoras, temos:







 Qual é o plural de lápis?
Qual é o plural de lápis? Gabarito oficial do Enem 2024: confira todos aqui
Gabarito oficial do Enem 2024: confira todos aqui Questão de Física do Enem 2024 é anulada; veja qual
Questão de Física do Enem 2024 é anulada; veja qual Confira nota de corte da Unicamp 2025 primeira fase
Confira nota de corte da Unicamp 2025 primeira fase 5 dicas de última hora para quem não leu os livros obrigatórios da Fuvest
5 dicas de última hora para quem não leu os livros obrigatórios da Fuvest