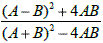Produtos Notáveis – Álgebra Básica
Soma de 2 termos elevada ao quadrado ( a + b )² = a² + 2ab + b² Diferença de 2 termos elevada ao quadrado ( a – b )² = a² – 2ab + b² Produto da soma pela diferença entre 2 termos ( a + b ).( a – b ) = a² – […]
Soma de 2 termos elevada ao quadrado
( a + b )² = a² + 2ab + b²
Diferença de 2 termos elevada ao quadrado
( a – b )² = a² – 2ab + b²
Produto da soma pela diferença entre 2 termos
( a + b ).( a – b ) = a² – b²
Soma de 3 termos elevada ao quadrado
( a + b + c )2 = a² + b² + c² + 2.( ab + ac + bc )
Soma de 2 termos elevada ao cubo
( a + b )³ = a³ + 3a2b + 3ab2 + b³
Diferença de 2 termos elevada ao cubo
( a – b )³ = a³ – 3a²b + 3ab² – b²
Produto de Stevin
( x + a ).( x + b ) = x² + ( a + b ).x + ab
Soma de 2 cubos
a³ + b³ = ( a + b ).( a² – ab + b² )
Diferença de 2 cubos
a³ – b³ = ( a – b ).( a² + ab + b² )
Macete! Os três primeiros produtos notáveis costumam cair com muito mais freqüência; portanto memorize-os bem (mas não esqueça dos outros).
Uma das maneiras desse conteúdo ser utilizado é na simplificação de expressões numéricas e algébricas.
Exemplo: Calcular o valor de 201² – 200²
Solução: 201² – 200² = (201 + 200).(201 – 200) = 401
Exemplo: Calcule 2010² – 2.2010.2009 + 2009²
Solução: 2010² – 2.2010.2009 + 2009² = (2010 – 2009)² = 1² = 1
Cuidado! Jamais substitua os números no lugar das letras de início para calcular expressões algébricas; primeiro simplifique-as ao máximo (reconhecendo produtos notáveis envolvidos) e então a substituição e alguns cálculos (poucos) serão feitos no final.
Exemplo: Se A = 5555 e B = 3333, então o valor da fração 
é:
a) 2
b) 32
c) 8
d) 4
e) 16
Solução: Letra e) pois basta ver que:
Solução: Fatorando o numerador, teremos:
Dica:
Uma ótima oportunidade de usar produtos notáveis é em demonstrações que envolvam divisibilidades.
(UNICAMP) Mostre que 3 divide n3 – n qualquer que seja o número natural n.
Solução: Fatorando, teremos: n3 – n = n.(n2 – 1) = (n – 1). n .(n + 1), que é o produto de três fatores consecutivos.
Logo, obrigatoriamente um dos três fatores é múltiplo de 3, portanto a demonstração está completa.
“Seriguela” ou “ciriguela”: qual o certo?
Participantes do Pé-de-Meia podem fazer o Enem de graça – e ainda receber por isso
Filmes que você não sabia mas são inspirados em Shakespeare
Por que perder a concentração às vezes ajuda a aprender
O problema simples da matemática que pode não ter solução
