Resumo de Física: Estática
A Estática é o capítulo da Mecânica que estuda corpos que não se movem, estáticos. A ausência de movimento é um caso especial de aceleração nula, ou seja, pelas Leis de Newton, uma situação em que todas as forças que atuam sobre um corpo se equilibram. Portanto, a soma vetorial de todas as forças que […]
A Estática é o capítulo da Mecânica que estuda corpos que não se movem, estáticos. A ausência de movimento é um caso especial de aceleração nula, ou seja, pelas Leis de Newton, uma situação em que todas as forças que atuam sobre um corpo se equilibram. Portanto, a soma vetorial de todas as forças que agem sobre o corpo deve ser nula.
Por exemplo, um edifício de apartamentos ou de escritórios está sujeito à força peso de sua massa e dos móveis e utensílios em seu interior, além da força peso da massa de todos os seus ocupantes. Existem também outras forças: a carga do vento, da chuva e eventualmente, em países frios, a carga da neve acumulada em seu teto. Todas essas forças devem ser absorvidas pelo solo e pelas fundações do prédio, que exercem reações sobre ele de modo a sustentá-lo, mantê-lo de pé e parado. A soma vetorial de todas essas forças deverá ser nula.
1. Equilíbrio do Ponto Material
Define-se como ponto material todo corpo cujas dimensões, para o estudo em questão, não são importantes, não interferem no resultado final. Por exemplo, o estudo da trajetória de um atleta de saltos ornamentais na piscina a partir de uma plataforma de 10 m. Se o estudo está focalizado na trajetória do atleta da plataforma até a piscina, e não nos seus movimentos em torno de si mesmo, pode-se adotar o centro de massa do atleta, ignorar seu tamanho e desenvolver o estudo. (Caso outros estudos, dos movimentos do atleta em torno do seu centro de massa, sejam necessários, eles poderão ser realizados posteriormente.)
Na Estática consideramos o ponto material como um corpo suficientemente pequeno para podermos admitir que todas as forças que agem sobre o corpo se cruzem num mesmo. Para que este ponto material esteja em equilíbrio a somatória vetorial das forças que nele atuam tem necessariamente de ser nula.
Ou:
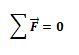
No caso do estudo se restringir ao plano, podemos adotar dois eixos (x e y) como referência e estudar as componentes das forças:
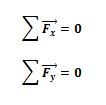
2. Equilíbrio dos Corpos Rígidos
Quando as dimensões dos corpos não podem ser ignoradas (não podemos considerar as forças todas se cruzando num mesmo ponto), o estudo passa a considerar movimentos de rotação. Por exemplo, na figura:
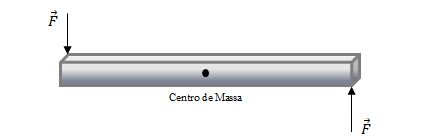
Sendo as forças de mesmo módulo, a resultante seria nula, mas isto seria insuficiente para o equilíbrio, pois existe uma tendência de giro que pode ser representado por:
A essa tendência de giro dá-se o nome de momento da força, e é igual à força multiplicada pela distancia ao centro de giro. No caso acima, supondo que o comprimento da barra seja x, o momento de cada força seria:
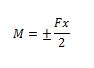
O momento total seria o dobro
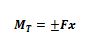
O sinal será definido pelo sistema de referência adotado: no nosso caso, adotando um sistema em que os momentos sejam positivos no sentido horário, o momento total seria negativo, pois o corpo tende a girar no sentido anti-horário:
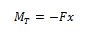
A unidade do momento de uma força é o newton∙metro ou N∙m.
Então, para o corpo permanecer estático, além das duas equações do ponto:
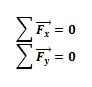
Uma terceira condição deve ser imposta: a somatória dos momentos deve ser nula:
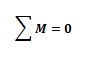
Nota: considera-se que todas as forças e momentos pertençam ao mesmo plano.
3. Alavancas
Ao se utilizar o princípio da estática e da somatória dos momentos nulos pode-se analisar uma das primeiras máquinas simples inventada pelo homem: a alavanca.
Veja o esquema abaixo onde a barra está equilibrada:
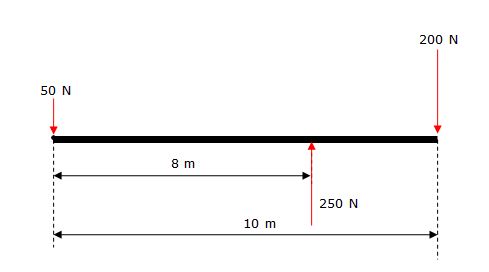
Nesse exemplo, ao se imaginar uma gangorra apoiada na distância de 8 m nota-se que uma força de 50N provoca uma ação na outra ponta de 200 N ampliando em 4 vezes a ação inicial. Para isto, basta comparar os momentos das duas forças nas extremidades em relação ao apoio, e constatar que eles se equilibram, pois têm o mesmo valor e sinais opostos (a força à esquerda tende a fazer a barra girar no sentido anti-horário e a da extremidade direita no sentido horário). Assim:
50 N x 8 m= 200 N x 2 m
Com isso pode-se amplificar ações de forças com a utilização dessa máquina simples, provavelmente pré-histórica.
| Exercícios |
|
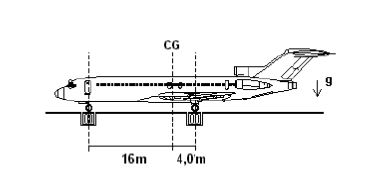
1. (Fuvest) Um avião, com massa M = 90 toneladas, para que esteja em equilíbrio em voo, deve manter seu centro de gravidade sobre a linha vertical CG, que dista 16 m do eixo da roda dianteira e 4,0 m do eixo das rodas traseiras, como na figura abaixo. Para estudar a distribuição de massas do avião, em solo, três balanças são colocadas sob as rodas do trem de aterrissagem. A balança sob a roda dianteira indica MD e cada uma das que estão sob as rodas traseiras indica MT. Uma distribuição de massas, compatível com o equilíbrio do avião em voo, poderia resultar em indicações das balanças, em toneladas, correspondendo aproximadamente a: a) MD = 0 MT = 45 |
|
2. (UECE) Duas forças concorrentes, ortogonais, de módulos 6 N e 8 N, respectivamente, admitem resultante de intensidade: a) 14 N |
|
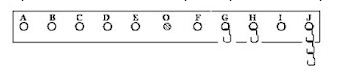
Colocam-se cinco ganchos idênticos, de peso P cada um, nos furos G, H e J na seguinte ordem: 1 em G; 1 em H e 3 em J. Para equilibrar a régua colocando outros cinco ganchos, idênticos aos já usados, num único furo, qual dos furos usaremos? a) A
|
Respostas:
1. c
2. b
3. b
O IBGE errou no mapa-múndi? Entenda o que determina o centro do mundo
“Coça” ou “cossa”: qual é o certo?
Clássico da literatura brasileira ganha versão em quadrinhos
“Xenófobo” ou “xenofóbico”: qual é o certo?
“Macete” ou “massete”: qual é o certo?
