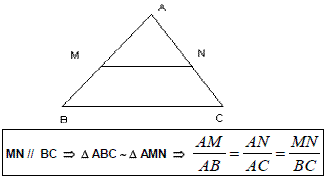
Semelhança
Geometria Básica
Por
SEGUIR
SEGUINDO
25 fev 2012, 13h17 • Atualizado em 16 Maio 2017, 13h49
Semelhança de Triângulos
Toda paralela a um dos lados de um triângulo determina outro triângulo semelhante, ou seja, a razão (proporção) entre seus lados é a mesma.
(FUVEST) No triângulo acutângulo ABC, a base AB mede 4cm e a altura relativa a essa base também mede 4cm. MNPQ é um retângulo cujos vértices M e N pertencem ao lado AB, P pertence ao lado BC e Q ao lado AC. O perímetro desse retângulo, em cm, é:
a) 4
b) 8
c) 12
d) 14
e) 16
Solução: Como MNPQ é retângulo, PQ é paralelo a AB e os triângulos ABC e QCP são semelhantes. Logo:
Cuidado! Em alguns exercícios a semelhança ocorre entre triângulos invertidos; então é preciso muita aten-ção na hora de “armar” a proporção correta.
(UFF) Considere o paralelogramo MNPQ represen-tado na figura abaixo. Se QT = 1/3 QP, então:
a) MV = ½ VP
b) MV = 3 VP
c) MV = 2 VP
d) MV = 2/9 VP
e) MV = 3/2 VP
Solução: Como MNPQ é paralelogramo, PQ é parale-lo a MN e os triângulos TPV e MNV são semelhantes.
Lembrando que QP = MN e PT = 2/3 QP, faremos:
Macete! A Regra do Z nos ajuda a visualizar os lados homólogos (que têm mesma posição); nesse exercício o lado MV é homólogo com VP.
Semelhança de Polígonos
Dois polígonos convexos são semelhantes se, e so-mente se todos os seus ângulos são congruentes e os lados homólogos (que têm mesma posição) são pro-porcionais.
Dica! Se dois polígonos são semelhantes, então a razão entre seus perímetros (soma dos lados) é igual a razão entre os lados homólogos.
(UNIFESP) A figura representa um retângulo subdividido em 4 outros retângulos com as respectivas áreas.
O valor de a é:
a) 4
b) 6
c) 8
d) 10
e) 12
Solução: As áreas dos retângulos semelhantes são proporcionais; portanto podemos fazer:
Letra b)
Dica! Uma segunda solução (mais simples…)
Como 8 = 4 x 2 e 9 = 3 x 3 não é difícil combinar os valores e ver que se 2a = 3 x 4, então a = 3 x 2 = 6.
Qual o coletivo de uva?
Luzinhas ou luzezinhas de Natal: qual é o plural?
O significado da palavra “frangalhos” – que não tem nada a ver com frango!
Por que dizer “assistir o filme” está errado, mesmo sendo tão comum no português
Qual é o coletivo de roupa?
