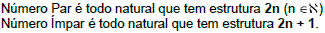Teoria dos Números – Aritmética Básica
Número Par é todo natural que tem estrutura 2n (n e N) Número Ímpar é todo natural que tem estrutura 2n + 1. (UERJ – 02) Analise a expressão abaixo, onde n é um número natural. a) Se n é um número par, então N também é um número par. Justifique sua resposta. Sistema […]

Número Par é todo natural que tem estrutura 2n (n e N)
Número Ímpar é todo natural que tem estrutura 2n + 1.
(UERJ – 02) Analise a expressão abaixo, onde n é um número natural. 
a) Se n é um número par, então N também é um número par. Justifique sua resposta.

Sistema Decimal de Numeração
Todo algarismo escrito a esquerda de outro, torna-o imediatamente 10 vezes superior ao situado a sua direita.
Exemplos:
27 = 2.10 + 7 → AB = 10. A + B
459 = 4.100 + 5.10 + 9 → ABC = 100.A + 10.B + C
(UFMG – 06) Sejam N um número natural de 2 alga-rismos não nulos e M o número obtido invertendo-se a ordem dos algarismos de N. Sabe-se que N – M = 45.
Então, quantos são os possíveis valores de N?
a) 7
b) 4
c) 5
d) 6

Dica! Resolva esse tipo de questão estipulando valores para as letras, sempre verificando possíveis restrições; não se preocupe e não tenha preguiça, pois geralmente são poucos casos a analisar.
Algoritmo da Divisão Euclidiana
O dividendo(D) é igual ao produto do divisor(d) pelo quociente(q) adicionando-se o resto(r).

O resto maior possível em uma divisão é igual ao divisor menos um, sendo o resto menor possível zero.
(UNIFESP – 03) Um número inteiro n, quando dividido por 7, deixa resto 5.
Qual será o resto na divisão de n2 + n por 7 ?
a) 5
b) 4
c) 3
d) 2
e) 1
Solução: Pelo algoritmo da divisão, n = 7q + 5.
Então: n2 + n = n.(n + 1) = (7q + 5).(7q + 6) = 49q2 + 77q + 30.
Como 49q2 e 77q são divisíveis por 7 (resto zero), basta fazer 30 → 7 que dá resto 2.
Letra d)
Macete! A Teoria das Congruências nos permite fazer contas com restos; ou seja, podemos achar facilmente o resto da questão da UNIFESP fazendo o seguinte:
n2 + n = 52 + 5 = 25 + 5 = 30 → 7 que dá resto 2
Princípio da Casa dos Pombos
Se n + 1 pombos são colocados em n casas, então pelo menos uma casa deverá conter dois ou mais pombos.
Exemplos:
O número mínimo de pessoas que devemos ter numa sala para que pelo menos duas comemorem aniversário no mesmo mês é 13, pois se tivéssemos 12 pessoas, na pior hipótese poderia cada uma fazer aniversário num mês diferente.
Num grupo de 15 pessoas, pelo menos 3 nasceram no mesmo dia da semana.
Verifique a pior hipótese na tabela abaixo:
(UERJ – 10) Uma máquina contém pequenas bolas de borracha de 10 cores diferentes, sendo 10 bolas de cada cor. Ao inserir uma moeda na máquina, uma bola é expelida ao acaso. Observe a ilustração:
Para garantir a retirada de 4 bolas de uma mesma cor, o menor número de moedas a serem inseridas na máquina corresponde a:
a) 5
b) 13
c) 31
d) 40
Solução: Imagine que ao retirar as 10 primeiras bolas, tivesse saído uma de cada cor (pior hipótese); ao retirar mais 10 bolas imagine que essa hipótese se repetiu e ao retirar mais 10 ocorre essa hipótese de novo. Teríamos retirado 30 bolas saindo as 10 cores em cada 3 bolas.
Se retirarmos uma 31ª bola qualquer teremos 4 bolas com mesma cor.
Letra c)
Macete! Imagine sempre a pior hipótese (a mais “aza-rada”) que pode ocorrer antes do pedido do problema se concretizar.
No caso da questão da UERJ o pior seria terem saído 3 bolas de todas as 10 cores (30 bolas ao todo); inevitavelmente a próxima bola resolve a questão!

 SEGUIR
SEGUIR
 SEGUINDO
SEGUINDO

 Qual é o coletivo de alho?
Qual é o coletivo de alho? Qual é o feminino de peru?
Qual é o feminino de peru? 4 motivos para repensar o uso do ChatGPT nos seus estudos
4 motivos para repensar o uso do ChatGPT nos seus estudos Conheça as únicas 3 escolas públicas do Brasil entre as 50 melhores no Enem 2024
Conheça as únicas 3 escolas públicas do Brasil entre as 50 melhores no Enem 2024 “Poça” ou “possa”: qual é o certo?
“Poça” ou “possa”: qual é o certo?