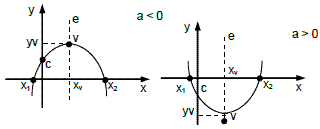Função Quadrática – Análise
É definida por y = f (x) = ax² + bx + c, sendo a ≠ 0. Gráfico da função É uma curva aberta chamada parábola que possui os seguintes elementos: Concavidade: para cima (a > 0) e para baixo (a < 0). Ponto (0,c): onde a parábola intercepta o eixo y (eixo das ordenadas) […]
É definida por y = f (x) = ax² + bx + c, sendo a ≠ 0.
Gráfico da função
É uma curva aberta chamada parábola que possui os seguintes elementos:
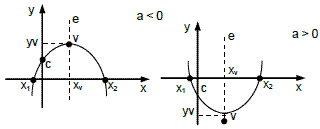
Concavidade: para cima (a > 0) e para baixo (a < 0).
Ponto (0,c): onde a parábola intercepta o eixo y (eixo das ordenadas)
Eixo de Simetria e: divide a parábola a partir do vérti-ce em pontos equidistantes.
Raízes (X1 e X2): a parábola intercepta o eixo x (eixo das abscissas)
Vértice (V): Ponto Máximo (a 0)
As coordenadas do vértice são dadas iguais pelas fórmulas: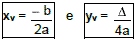
(UFF) A equação da parábola que passa por (-2,0) e cujo vértice situa-se no ponto (1,3) é:
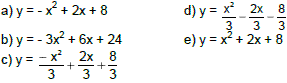
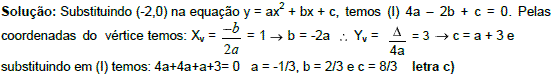
Problemas de Máximos e Mínimos
Devem ser tomadas duas providências:
1º) Montar a função quadrática;
2º) Calcular as coordenadas do vértice (Xv ou Yv)
(FUVEST) Uma caixa d`água tem a forma de paralele-pípedo reto-retângulo , cujas medidas internas são, em m, “x”, ” 20 – x” e “2”. O maior volume, em m³, que ela poderá conter é igual a:
a) 150
b) 200
c) 220
d) 250
Solução: Valor do Volume: V = 2x.(20 – x)= – 2x² + 40x
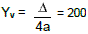
Letra b)

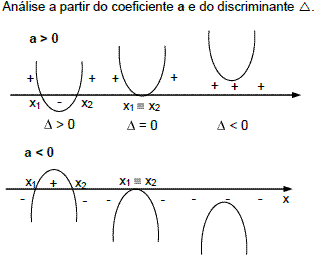
Estudo do Sinal da Função Quadrática:
(UFF) Determine o domínio da função real de variável real f, definida por:
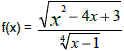



 “Murcha” ou “mucha”: qual é o certo?
“Murcha” ou “mucha”: qual é o certo? O que são cometas?
O que são cometas? Enem 2024: último dia para pedir isenção da taxa de inscrição
Enem 2024: último dia para pedir isenção da taxa de inscrição “Seriguela” ou “ciriguela”: qual o certo?
“Seriguela” ou “ciriguela”: qual o certo? “Guerra Civil”: o que o filme com Wagner Moura ensina sobre História e política
“Guerra Civil”: o que o filme com Wagner Moura ensina sobre História e política