O que é plano cartesiano, e para que serve
Ferramenta de uso simples hoje em dia, sua criação há quatro séculos foi fundamental para o desenvolvimento da matemática e da física
Um plano cartesiano é uma criação simples que permite localizar qualquer ponto numa superfície plana. Hoje parece uma coisa banal. Mas a sua criação pelo genial filósofo francês René Descartes (1596-1650), unindo álgebra e geometria, forneceu uma importante ferramenta para o desenvolvimento da matemática e da física modernas.
Num plano cartesiano, cruzam-se duas retas: a horizontal é a das abscissas (representada também como o eixo x); a vertical é a das ordenadas (eixo y). Veja a representação abaixo. Para facilitar, o fundo está quadriculado em espaços iguais, correspondentes às marcações nas retas: 1, 2, 3… As retas, por definição, são perpendiculares, ou seja, seu cruzamento produz quadro ângulos retos (ângulos de 90º). Note que, no cruzamento das duas retas, a contagem começa a partir do zero, tanto positiva – para cima e para a direita –, quanto negativa – para baixo e para a esquerda.
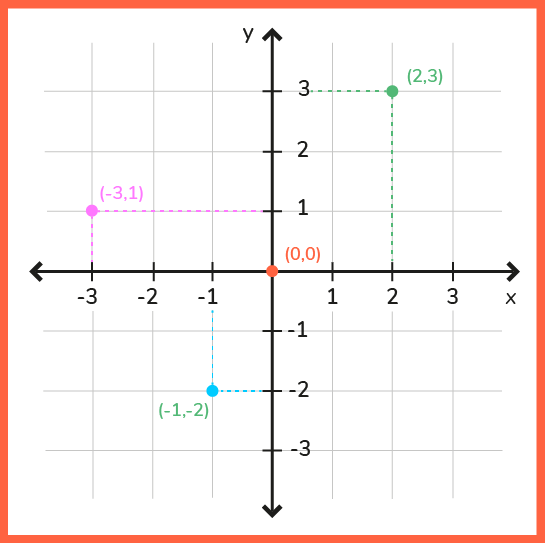
Veja abaixo como se dá a representação de 4 diferentes pontos no plano cartesiano, sempre com o número da abscissa vindo em primeiro:
[entra a ilustração]
- o primeiro é o (0,0): está na junção das duas retas.
- o segundo é o (2,3), com dois valores positivos.
- o terceiro é o (-3,1), com o valor negativo à esquerda do eixo y.
- o quarto é o (-1,-2), com os dois valores negativos.
Perceba que, nesse plano cartesiano, qualquer ponto pode ser localizado, e tem uma localização única. O plano cartesiano possui pontos infinitos.
+ Teorema de Pitágoras: o que é, a fórmula e como usar
Alguns usos do plano cartesiano
Como o plano cartesiano permite localizar qualquer ponto numa superfície plana, então permite localizar também qualquer reta, curva, círculo ou forma geométrica nessa superfície, pois as linhas são junções de pontos. Por exemplo, você tem o ponto (2,3) e o ponto (4,5). Se ligá-los de forma direta, terá uma reta.
Ao colocar a reta no plano cartesiano, você também consegue calcular o tamanho dessa reta. Vamos considerar os pontos A (localizado pela junção de Xa e Ya) e B (junção de Xb e Yb), e a reta que os liga.
Vamos usar o plano cartesiano para calcular a extensão dessa reta, com o auxílio do Teorema de Pitágoras (filósofo e matemática grego, que viveu há 2.500 anos). Pelo teorema, num triângulo retângulo (aquele em que dois lados, chamados de catetos, formam um ângulo reto), quando você eleva ao quadrado o comprimento dos catetos, e os soma, o resultado é igual ao quadrado da hipotenusa (que é a terceira reta do triângulo, oposta ao ângulo reto).
Sua fórmula é: a soma do quadrado dos catetos é igual ao quadrado da hipotenusa.
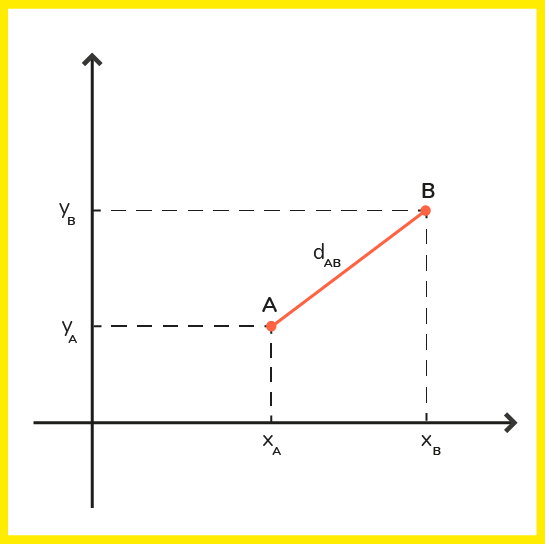
Veja abaixo a reta entre os pontos A e B, batizada de dAB.
Então, com o auxílio do plano cartesiano, podemos traçar um triângulo reto, tornando a reta dAB a hipotenusa do triângulo, como mostra o esquema abaixo, e criando o ponto P (Xb, Ya).
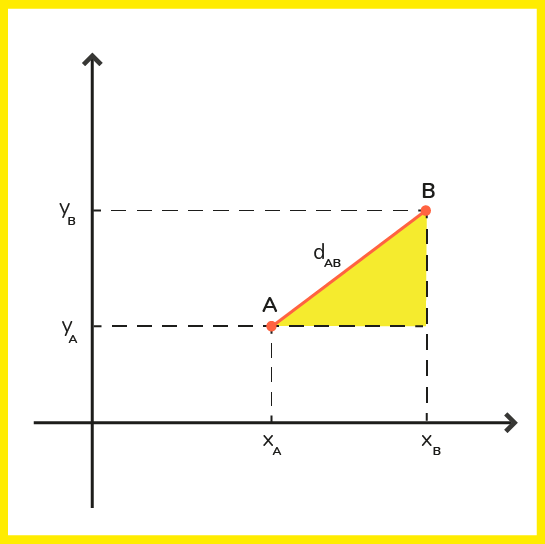
Então, usando o Teorema de Pitágoras, temos o seguinte raciocínio:
– No triângulo ABP
- a reta dAB é a hipotenusa, da qual queremos descobrir a medida;
- a medida do cateto AP é determinada por (Xb – Xa);
- a medida do cateto BP é determinada por (Yb – Ya);
- portanto, a medida da reta dAB² = (Xb – Xa)² + (Yb – Ya)²
- ou ainda, dAB = raiz quadrada de (Xb – Xa)² + (Yb – Ya)²
Veja, portanto, que o plano cartesiano permite representar equações matemáticas.
+ Revisão para o Enem: saiba como calcular uma porcentagem
Plano cartesiano e gráficos
No exemplo a seguir, vemos uma utilização bem comum do plano cartesiano: é usado como base de um gráfico de linhas (ou de barras) para expressar um fenômeno numérico. No caso abaixo, o crescimento da população brasileira medida nos 13 Censos realizados até hoje.
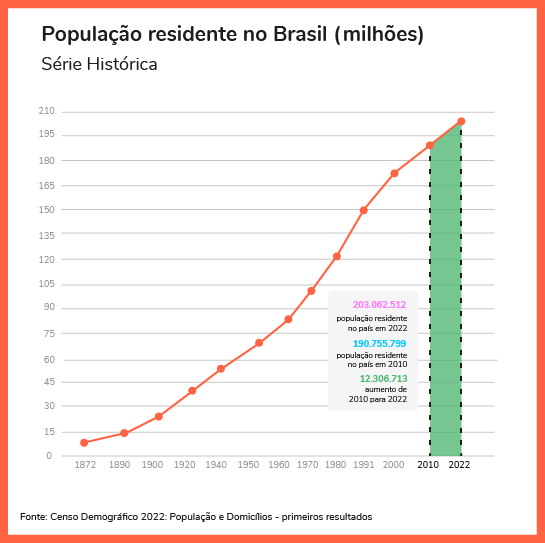
A reta das abscissas registra os anos dos 13 Censos (de 1872 a 2022). A reta das ordenadas mostra o tamanho da população brasileira, em milhões de pessoas: na primeira contagem, em 1872, eram pouco mais de 9 milhões de habitantes; na última, 203 milhões.
Note que, apenas olhando o gráfico, percebe-se que o crescimento da população acelerou a partir de 1950, e começou a frear devagar a partir de 1991. O gráfico destaca o crescimento da população no último intervalo de tempo (2010 a 2022), com aumento de pouco mais de 12 milhões de pessoas.
Gráficos semelhantes, tendo como base o plano cartesiano, mostram a variação da inflação ou dos preços de alguns produtos (às vezes com números negativos), a evolução do número de doentes numa epidemia ou o desempenho de times de futebol ao longo de um campeonato por pontos, além de muitas outras coisas. Como se vê, o plano cartesiano é pau para toda obra!
Prepare-se para o Enem sem sair de casa. Assine o Curso GUIA DO ESTUDANTE ENEM e tenha acesso a todas as provas do Enem para fazer online e mais de 180 videoaulas com professores do Poliedro, recordista de aprovação nas universidades mais concorridas do país.
“A champanhe” ou “o champanhe”: qual o certo?
O que define as profissões que serão ou não substituídas pela Inteligência Artificial?
3 técnicas de memorização para deixar seu cérebro afiado
O que é a “revolução das skills” e como se preparar para ela
Relembre as notas de corte do Enem-USP 2024
